Question

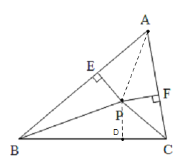
【题目】已知：如图，在△ABC中，∠ABC和∠ACB的角平分线相交于点P，且PE⊥AB，PF⊥AC，垂足分别为E、F

（1）求证：PE=PF；

（2）若∠BAC=60°，连接AP，求∠EAP的度数.

Answer 1

【答案】（1）见解析；（2）30°.

【解析】

（1）作PD⊥BC于点D，根据角平分线的性质知PD=PE，PD=PF，从而证明PE=PF即可；

（2）∠ABC和∠ACB的角平分线相交于点P，则AP平分∠BAC，即可求出∠EAP的度数.

（1）作PD⊥BC于点D，

∵BP平分∠ABC，CP平分∠ACB，PE⊥AB，PF⊥AC，

∴PD=PE，PD=PF，

∴PE=PF；

（2）∵∠ABC和∠ACB的角平分线相交于点P，

∴AP平分∠BAC，

∵∠BAC=60°，

∴∠EAP=30°.