��Ŀ����
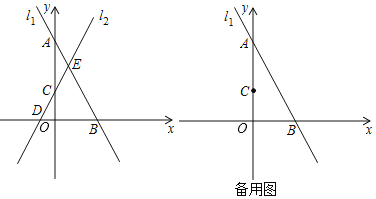
����Ŀ������ѧ�����,����ʦ��ͬѧ�������ýdz�ƽ�� ![]() (��ͼ��ʾ),�����飮
(��ͼ��ʾ),�����飮
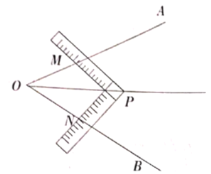
ͬѧ��������·���:
������:���dzߵ�ֱ�Ƕ���![]() ��������
��������![]() ֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶�λ��
֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶�λ��![]() ��,�ҽ���ֱ�Ϊ
��,�ҽ���ֱ�Ϊ![]() ,��
,��![]() ,���dz߶���
,���dz߶���![]() ������
������![]() ����
����![]() ��ƽ���ߣ�
��ƽ���ߣ�
������:�ڱ�![]() �Ϸֱ��ȡ
�Ϸֱ��ȡ![]() ,���dzߵ�ֱ�Ƕ���
,���dzߵ�ֱ�Ƕ���![]() ��������
��������![]() ֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶����
֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶����![]() �غ�,��
�غ�,��![]() ,���dz߶���
,���dz߶���![]() ������
������![]() ����
����![]() ��ƽ����.��ֱ�˵���������뷽�����Ƿ����?������,��֤��; �������У���˵�����ɣ�
��ƽ����.��ֱ�˵���������뷽�����Ƿ����?������,��֤��; �������У���˵�����ɣ�
���𰸡������ٲ����У����ɼ������������ڿ��У�֤����������
��������
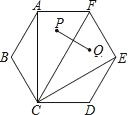
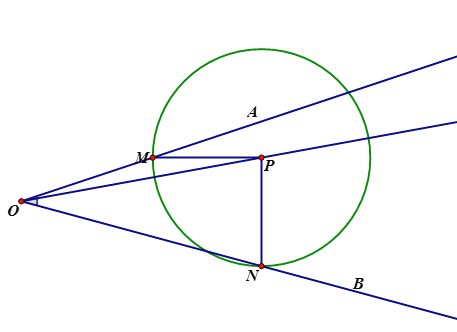
ͨ����ͼ�ɷ����������������ж�PM=PN�������ж�PO���ǡ�AOB�Ľ�ƽ���ߣ��ؼ���ȱ�١�OPM�ա�OPN��������ֻ�����߱�����������
�������С�OPM�͡�OPN��ȫ�������Σ�������ȣ������MOP=��NOP������OPΪ��AOB�Ľ�ƽ���ߣ�
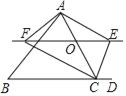
��ͼ�ɵã�������������.
��Ϊֻ��![]() ,�����ж�
,�����ж�![]() .
.
���ܵõ�![]() ,���Բ����ж�
,���Բ����ж�![]() ����
����![]() ��ƽ����.
��ƽ����.
����������.
��![]() ��
��![]() ��
�У�
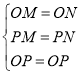
![]()
![]() .
.
![]() ����
����![]() ��ƽ����.
��ƽ����.

����Ŀ��ij����������˾�ṩ���ֻ��ͻ�Ա������֧����ʽ�������ֻ�֧����ʽ������ʱ���ڰ�Сʱ���ڣ�����Сʱ�����շѣ�������Сʱ��ÿ��Сʱ�շ�1Ԫ����ѡ���Ա��֧��������ʱ��ÿ��Сʱ�շ�0.8Ԫ��������ʱ��ΪxСʱ��
��1���������⣬��д�±�����λ��Ԫ����
����ʱ�䣨Сʱ�� | 0.5 | 2 | 3 | �� |
�ֻ�֧�������Ԫ�� | 0 | �� | ||
��Ա��֧�������Ԫ�� | 3.2 | �� |
��2�������ֻ�֧��������Ϊy1Ԫ���û�Ա��֧��������Ϊy2Ԫ���ֱ�д��y1��y2����x�ĺ�����ϵʽ��
��3��������ʦ�������иù�˾�Ĺ�����������Ӧѡ������֧����ʽ�ȽϺ��㣿