题目内容
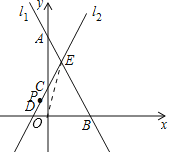
【题目】在平面直角坐标系中，直线l1：y＝﹣2x+6与坐标轴交于A，B两点，直线l2：y＝kx+2（k＞0）与坐标轴交于点C，D，直线l1，l2与相交于点E．
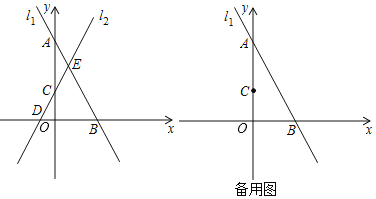
（1）当k＝2时，求两条直线与x轴围成的△BDE的面积；
（2）点P（a，b）在直线l2：y＝kx+2（k＞0）上，且点P在第二象限．当四边形OBEC的面积为
时．
①求k的值；
②若m＝a+b，求m的取值范围．
【答案】（1）△BDE的面积＝8；（2）①k＝4；②﹣
＜m＜2．
【解析】
（1）由直线l1的解析式可得点A、点B的坐标，当k＝2时，由直线l2的解析式可得点C、点D坐标，联立直线l1与直线l2的解析式可得点E坐标，根据三角形面积公式求解即可；
（2）①连接OE．设E（n，﹣2n+6），由S四边形OBEC＝S△EOC+S△EOB可求得n的值，求出点E坐标，把点E代入y＝kx+2中求出k值即可；②由直线y＝4x+2的表达式可确定点D坐标，根据点P（a，b）在直线y＝4x+2上，且点P在第二象限可得
及
的取值范围，由m＝a+b可确定m的取值范围.
解：（1）∵直线l1：y＝﹣2x+6与坐标轴交于A，B两点，
∴当y＝0时，得x＝3，当x＝0时，y＝6；
∴A（0，6）B（3，0）；
当k＝2时，直线l2：y＝2x+2（k≠0），
∴C（0，2），D（﹣1，0）
解
得
，
∴E（1，4），
，点E到x轴的距离为4，
∴△BDE的面积＝×4×4＝8．
（2）①连接OE．设E（n，﹣2n+6），
∵S四边形OBEC＝S△EOC+S△EOB，
∴×2×n+×3×（﹣2n+6）＝
，
解得n＝
，
∴E（，
），
把点E代入y＝kx+2中，＝k+2，
解得k＝4．
②∵直线y＝4x+2交x轴于D，
∴D（﹣，0），
∵P（a，b）在第二象限，即在线段CD上，
∴﹣＜a＜0，
∵点P（a，b）在直线y＝kx+2上
∴b＝4a+2，
∴m＝a+b＝5a+2，
∴﹣＜m＜2．
