题目内容
【题目】已知:一次函数的表达式为y=![]() x﹣1
x﹣1
(1)该函数与x轴交点坐标为 ,与y轴的交点坐标为 ;
(2)画出该函数的图象(不必列表);
(3)根据该函数的图象回答下列问题:
①当x 时,则y>0;
②当﹣2≤x<4时,则y的取值范围是 .
【答案】(1)(2,0),(0,﹣1);(2)详见解析;(3) x>2,﹣2≤y<1
【解析】
(1)把y=0代入y=![]() 得到关于x的一元一次方程,解之,即可得到该函数与x轴交点坐标,把x=0代入y=
得到关于x的一元一次方程,解之,即可得到该函数与x轴交点坐标,把x=0代入y=![]() 得到关于y的一元一次方程,解之,即可得到该函数与y轴交点坐标,
得到关于y的一元一次方程,解之,即可得到该函数与y轴交点坐标,
(2)结合(1)的结果,标出该函数与x轴和y轴的交点,连接两点并延长,即可得到该函数的图象,
(3)由图象可知:该函数的图象上的点y随着x的增大而增大,求出y=0时,x=2;x=﹣2与x=4时y的值,根据图像即可求解.
解:(1)把y=0代入y=![]() 得:
得:![]() ,
,
解得:x=2,
即该函数与x轴交点坐标为(2,0),
把x=0代入y=![]() 得:y=﹣1,
得:y=﹣1,
即该函数与y轴的交点坐标为(0,﹣1),
故答案为:(2,0),(0,﹣1),
(2)标出点(2,0)和点(0,﹣1),连接两点并延长,即可得到该函数的图象,
如下图所示:
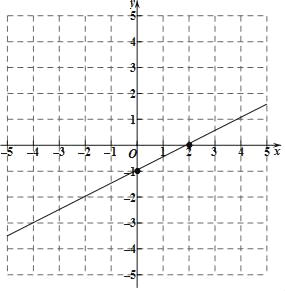
(3)由图象可知:该函数的图象上的点y随着x的增大而增大,
当y=0时,x=2,
即当x>2时,y>0,
把x=﹣2代入y=![]() ﹣1得:y=
﹣1得:y=![]() ×(﹣2)﹣1=﹣2,
×(﹣2)﹣1=﹣2,
把x=4代入y=![]() 得:y=
得:y=![]() ﹣1=1,
﹣1=1,
即当﹣2≤x<4时,y的取值范围是﹣2≤y<1,
故答案为:x>2;﹣2≤y<1.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目