Question

【题目】如图，等腰△ABC中，AB=AC=，BC=4，点B在y轴上，BC∥x轴，反比例函数（x>0）的图像经过点A，交BC于点D．

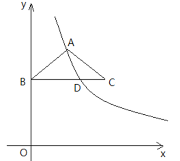
（1）若OB=3，求k的值；

（2）连接CO，若AB=BD，求四边形ABOC的周长．

Answer 1

【答案】（1）k=9；（2）.

【解析】

（1）过点A作AH⊥BC于点H，求出AH和BH的长，即可确定A点坐标，从而求出k的值；

（2）设B点坐标为（0，a），写出A，D两点的坐标，根据A，D都在反比例函数上，求出a，k的值，从而求出周长.

解：（1）过点A作AH⊥BC于点H，

∵AB=AC=，BC=4，

∴BH=，

在Rt△ABH中，

，

∵OB=3，

∴A点坐标为，

把A代入反比例函数中，得，

解得：k=9；

（2）设B点坐标为（0，a），

∵BD=AB，

∴D点坐标为，

∴A点坐标为，

∵反比例函数经过A，D两点，

∴把A，D两点代入反比例函数中，得：，

解得：，

则D点坐标为，A点坐标为，

在Rt△OBC中，

，

∴四边形ABOC的周长为.