题目内容
【题目】如图，∠AOB=45°，点M，N在边OA上，OM=3，ON=7，点P是直线OB上的点，要使点P，M，N构成等腰三角形的点P有________个．
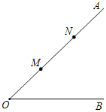
【答案】3
【解析】
先求出点M、N到在OB的距离，再根据等腰三角形的判定逐个画出即可．
解：
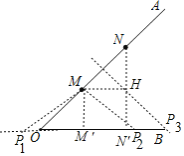
过M作MM′⊥OB于M′，过N作NN′⊥OB于N′，
∵OM=3，ON=7，∠AOB=45°，
∴MN=4，MM′=OM×sin45°=
＜4，NN′=ON×sin45°=
＞4，MH=M′N′=4×sin45°=2
＜4，
所以只有一小两种情况：①以M为圆心，以4为半径画弧，交直线OB于P1、P2，此时△NP1M和△NMP2都是等腰三角形；
②作线段MN的垂直平分线，交直线PB于P3，此时△MNP3是等腰三角形，
即有3个点P符合，
故答案为：3．
练习册系列答案
相关题目
