题目内容
【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上. 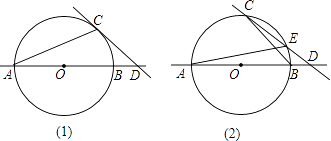
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
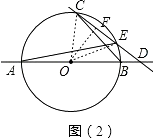
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次?
【答案】
(1)证明:如图(1),连接OC,
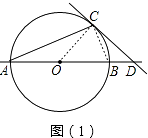
∵OA=OC,
∴∠OAC=∠OCA,
又∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠BCD=∠BAC=∠OCA,
∴∠BCD+∠OCB=90°,即OC⊥CD,
∴CD是⊙O的切线
(2)解:∵∠ADE=∠CDB,∠BCD=∠EAD,
∴△BCD∽△EAD,
∴ ![]() ,
,
∴ ![]() ,
,
又∵BD:DE:EC=2:3:5,⊙O的半径为5,
∴BD=2,DE=3,EC=5,
如图(2),连接OC、OE,则△OEC是等边三角形,
作OF⊥CE于F,则EF= ![]() CE=
CE= ![]() ,∴OF=
,∴OF= ![]() ,
,
∴圆心O到直线CD的距离是 ![]() .
.
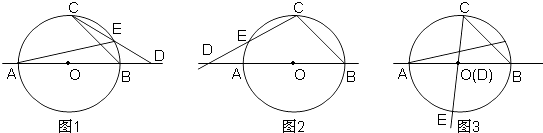
(3)解:这样的情形共有出现三次:
当点D在⊙O外时,点E是CD中点,有以下两种情形,如图1、图2;
当点D在⊙O内时,点D是CE中点,有以下一种情形,如图3.
【解析】(1)连接OC,根据弦切角定理和圆的性质可得到∠BCD=∠BAC=∠OCA,结合圆周角定理可求得∠OCD=90°,可证明CD是切线;(2)先证明△BCD∽△EAD,结合条件可求得BD=2,DE=3,EC=5,在△OBC中可求得O到CD的距离;(3)分点D在⊙O外和点D在⊙O内两种情况,当D在⊙O外时又分D在A点左边和D在B点右边两种情况,当D在⊙O内时只有一种,结合图形可给出答案.

练习册系列答案
相关题目