题目内容
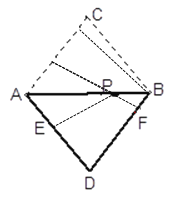
【题目】如图，在△ABC中，AC=BC=5，AB=6,将它沿AB翻折得到△ABD，点P、E、F分别为线段AB、AD、DB的任意点，则PE+PF的最小值是________．
【答案】
【解析】
根据题意证明四边相等即可得出菱形；作E关于AB的对称点E' ，连接E'F交AB于点P，交ABA于点P, 当E'F是AC，BD之间的距离时，E'F为最小.过点B作BH⊥AC于点H，求出BH的长即可.
∵AD=BD=AC= BC，∴四边形ADBC是菱形；
如解图,作E关于AB的对称点E' ，根据菱形的对称性可知点E'在AC上，连接E'F交AB于点P，PE+PF=PE' +PF=E'F,当E'F是AC，BD之间的距离时，E'F为最小.过点B作BH⊥AC于点H，设AH=x，则CH=5 -x，由AB2－AH2 =BH2=BC2－CH2，得62 –x2 =25－(5－x)2，解得x＝
，∴BH =
，PE + PF的最小值为.故答案为.
练习册系列答案
阅读快车系列答案
相关题目
