题目内容
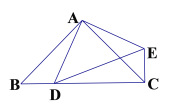
【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.

【答案】(1)10;(2)![]()
【解析】
(1)在△BCD中,由勾股定理逆定理可得△BCD是直角三角形,即∠ADB=90°,直角三角形斜边上的中线等于斜边的一半可解得线段DE的长;
(2) 当DE⊥AB时,DE有最小值.根据等面积法即可求出DE的长.
解:(1)∵AC=21,AD=16,
∴CD=21-16=5,
∵DC +BD =5 +12 =169,BC =13 =169,
∴DC +BD = BC ,
∴△BCD是直角三角形。且∠BDC=90°,
∴∠ADB=90°,
在Rt△ADB中,由勾股定理得AB=![]() =20,
=20,
∵∠ADB=90°,E为斜边AB的中点,
∴DE=![]() AB=
AB=![]() ×20=10.
×20=10.
(2)当DE⊥AB时,DE有最小值.
此时AB×DE=AD×DB,即20DE=16×12,
解得DE=![]() .
.

练习册系列答案
相关题目
【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别 | 成绩x(分数) | 组中值 | 频数(人数) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.