题目内容
【题目】已知在平面直角坐标系中,已知A(3,4),B(3,﹣1),C(﹣3,﹣2),D(﹣2,3)
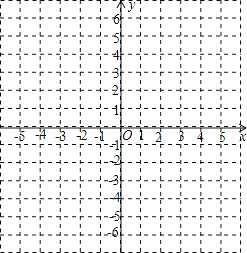
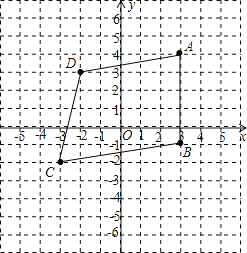
(1)在图上画出四边形ABCD,并求四边形ABCD的面积;
(2)若P为四边形ABCD形内一点,已知P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),根据平移的规则,请直接写出四边形ABCD平移后的四个顶点的坐标.
【答案】(1)画图见解析,面积为27;(2)平移后的点坐标A(6,1),B(6,﹣4),C(0,﹣5),D(1,0).
【解析】
试题分析:(1)在坐标系内描出各点,再顺次连接,利用矩形的面积减去三角形与正方形的面积即可;
(2)根据P点坐标的变化写出各点坐标即可.
解:(1)如图所示.
S四边形ABCD=6×6﹣![]() ×6×1﹣
×6×1﹣![]() ×5×1﹣
×5×1﹣![]() ×5×1﹣1
×5×1﹣1
=36﹣3﹣![]() ﹣
﹣![]() ﹣1
﹣1
=36﹣3﹣5﹣1
=27;
(2)∵P坐标为(﹣1,1),将四边形ABCD通过平移后,P的坐标变为(2,﹣2),
∴平移后各点横坐标加3,纵坐标减3,
∴平移后的点坐标A(6,1),B(6,﹣4),C(0,﹣5),D(1,0).

练习册系列答案
相关题目