��Ŀ����
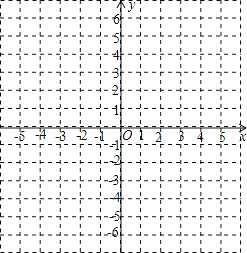
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��0��������B��b��������������b���㣨a��2��2+|b��4|=0����ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��
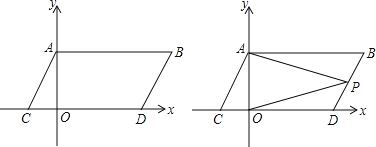
��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD
��2����y�����Ƿ����һ��M������MC��MD��ʹS��MCD=S�ı���ABDC������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����P���߶�BD�ϵ�һ�����㣬����PA��PO������P��BD���ƶ�ʱ������B��D�غϣ�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
���𰸡���1��S�ı���ABDC=8����2�����ڣ�M��0��4����0����4������3�����䣬���ɼ�����.
��������
�����������1�����ɷǸ����������a=2��b=4���ٸ���ƽ�ƹ��ɣ��ó���C��D�����꣬Ȼ������ı���ABDC�����=AB��OA������⣻
��2�����ڣ���M����Ϊ��0��m��������S��PAB=S�ı���ABDC���г��������m��ֵ������ȷ��M�����ꣻ
��3����P����PE��AB��OC��E�㣬����ƽ���ߵ����ʵ���BAP+��DOP=��APE+��OPE=��APO���ʱ�ֵΪ1��
�⣺��1������a��2��2+|b��4|=0��
��a=2��b=4��
��A��0��2����B��4��2����
������A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D��
��C����1��0����D��3��0����
��S�ı���ABDC=AB��OA=4��2=8��
��2����y���ϴ���һ��M��ʹS��MCD=S�ı���ABCD����M����Ϊ��0��m����
��S��MCD=S�ı���ABDC��
��![]() ��4|m|=8��
��4|m|=8��
��2|m|=8��
���m=��4��
��M��0��4����0����4����
��3������P��BD���ƶ�ʱ��![]() =1���䣬�������£�
=1���䣬�������£�
����P��PE��AB��OA��E��
��CD��ABƽ�Ƶõ�����CD��AB��
��PE��CD��
���BAP=��APE����DOP=��OPE��
���BAP+��DOP=��APE+��OPE=��APO��
��![]() =1��
=1��