题目内容
【题目】教材呈现：下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形，线段的垂直一部分线是线段的对称轴，如图直线
是线段
的垂直平分线，
是上任一点，连结
、
，将线段与直线对称，我们发现与完全重合，由此都有：线段垂直平分线的性质定理，线段垂直平分线上的点到线段的距离相等.
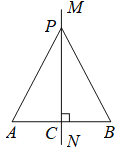
已知：如图，
，垂足为点
，
，点是直线上的任意一点.
求证：
.
图中的两个直角三角形
和
，只要证明这两个三角形全等，便可证明（请写出完整的证明过程）
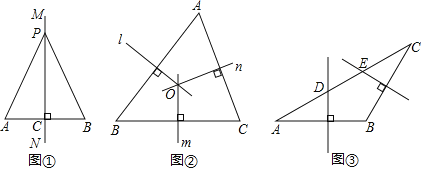
请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程，定理应用.
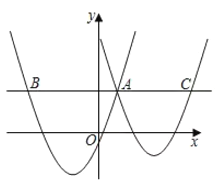
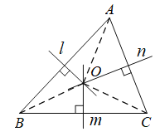
（1）如图②，在
中，直线
、
、
分别是边、
、
的垂直平分线.
求证：直线、、交于点.
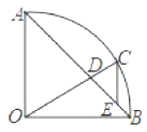
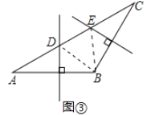
（2）如图③，在中，
，边的垂直平分线交于点
，边的垂直平分线交于点
，若
，
，则
的长为_______.
【答案】教材呈现：详见解析；定理应用：（1）详见解析；（2）6.
【解析】
教材呈现： 
得到
，从而
定理应用：（1）连结
、
、
．设直线
、
交于点
．因为直线是边
的垂直平分线，所以
又因直线是边
的垂直平分线，
得到
点在边
的垂直平分线
上．得到直线、、交于点． （2）
连接BD，BF，易知AD=DB，BE=EC；又因为∠A=∠C=30°，得到∠DBE=60°，所以∠ABD=30°，得到∠BDE=60°，所以△BED为等边三角形，所以DE=
AC=6
教材呈现：
，
又
．
图① 图②
定理应用：
（1）连结、、．
设直线、交于点．
直线是边的垂直平分线，
又直线是边的垂直平分线，
在边的垂直平分线上．
直线、、交于点．
（2）如图3，连接BD,BF
由第一问可知，AD=DB，BE=EC，∠A=∠DBA，∠C=∠CBE
∵AB=AC
∴∠A=∠C
∵∠ABC=120°
∴∠A=∠C=30°
∴∠A=∠DBA=∠C=∠CBE=30°
∴∠BDE=∠A+∠ABD=60°，∠DBE=∠ABC-∠ABD-∠EBC=60°
∴△DBE是等边三角形
∴DB=BE=DE
∴AD=DE=EC
∴DE=AC=6
名校课堂系列答案
