题目内容
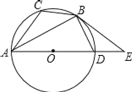
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
⑴求证:BE是⊙O的切线;
⑵若BC=![]() ,AC=5,求圆的直径AD的长.
,AC=5,求圆的直径AD的长.
【答案】(1)详见解析;(2)6
【解析】
(1)先根据等弦所对的劣弧相等,再结合∠EBD=∠CAB从而得到∠BAD=∠EBD,最后用直径所对的圆周角为直角即可;
(2)利用三角形的中位线先求出OM,再用勾股定理求出半径r,最后得到直径的长.
解:⑴证明:连接OB,CD,OB、CD交于点M
∵BC=BD,

∴∠CAB=∠BAD.
∵OA=OB,
∴∠BAD=∠OBA.
∴∠CAB=∠OBA.
∴OB∥AC.
又AD是直径,
∴∠ABD=∠ACD =90°,
又∠EBD=∠CAB, ∠CAB=∠OBA.
∴∠OBE=90°,即OB⊥BE.
又OB是半径,
∴BE是⊙O的切线.
⑵∵ OB∥AC, OA=OD,AC=5,.
∴ OM=2.5 ,BM=OB-2.5,OB⊥CD
设⊙O的半径为r,则
在Rt△OMD中:MD2=r2-2.52;
在Rt△BMD中:MD2=BD2-(r-2.5)2 ,BD=BC=![]() .
.
∴r1=3 ,r2=-0.5(舍).
∴圆的直径AD的长是6.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目