��Ŀ����
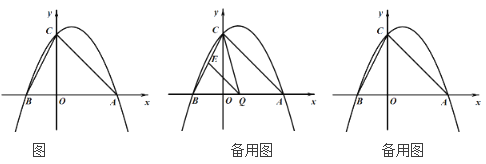
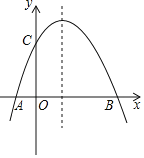
����Ŀ����ͼ�ף�������y��ax2+bx��1����A����1��0����B��2��0�����㣬��y���ڵ�C��
��1���������ߵı���ʽ��ֱ��BC�ı���ʽ��
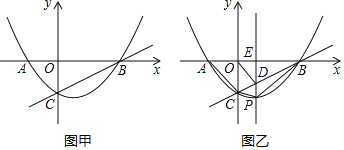
��2����ͼ�ң���PΪ�ڵ����������������ϵ�һ�����㣬����P��x��Ĵ���PE��ֱ��BC�ڵ�D��
���ڵ�P�˶������У��ı���ACPB������Ƿ�������ֵ�������ڣ����������ֵ���������ڣ�˵�����ɣ�
���Ƿ���ڵ�Pʹ���Ե�O��C��DΪ������������ǵ��������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1�������ߵı���ʽΪ��![]() ��ֱ��BC�ı���ʽΪ��y��
��ֱ��BC�ı���ʽΪ��y��![]() x��1����2�������ڣ����ֵΪ2������
x��1����2�������ڣ����ֵΪ2������![]() ��
��![]() ����1����1����
����1����1����![]() ����
����![]() ����
����
��������
(1) ����κ����ı���ʽΪ��y��a��x+1����x��2����ax2��ax��2a��������2a����1��������⣻�ô���ϵ�����������ֱ��BC�ı���ʽ��
(2) ��S�ı���ACPB��S��ABC+S��BCP��![]() ��AB��OC+
��AB��OC+![]() ��PD��OB��������⣻
��PD��OB��������⣻
����CD��OC��CD��OD��OC��OD��������ֱ���⼴�ɣ�
�⣺��1�����κ����ı���ʽΪ��y��a��x+1����x��2����ax2��ax��2a��
������2a����1����ã�a��![]() ��
��
�������ߵı���ʽΪ��![]() ����C��0����1����
����C��0����1����
��ֱ��BC�ı���ʽΪ��y��kx��1��
����B�����������ʽ�ã�0��2k��1����ã�k��![]() ��
��
��ֱ��BC�ı���ʽΪ��y��![]() x��1��
x��1��
��2�������P��x��![]() x2��
x2��![]() x��1�������D��x��
x��1�������D��x��![]() x��1����
x��1����
S�ı���ACPB��S��ABC+S��BCP��![]() ��AB��OC+
��AB��OC+![]() ��PD��OB
��PD��OB
��![]() ��3��1+
��3��1+![]() ��2��
��2��![]() x��1��
x��1��![]() x2+
x2+![]() x+1������
x+1������![]() x2+x+
x2+x+![]() ��
��
�ߩ�![]() 0����S�����ֵ����x��1ʱ��S���ֵΪ2��
0����S�����ֵ����x��1ʱ��S���ֵΪ2��
�����D������m��![]() m��1����
m��1����
��CD2��m2+![]() m2��OC2��1��DO2��m2+��
m2��OC2��1��DO2��m2+��![]() m��1��2��
m��1��2��![]() m2��m+1��
m2��m+1��
��CD��OCʱ��m2+![]() m2��1����ã�m��
m2��1����ã�m��![]() ��
��
ͬ���ɵã�
��CD��ODʱ��m��1��
��OC��ODʱ��m��![]() ��
��
���P������![]() ��
��![]() ����1����1����
����1����1����![]() ����
����![]() ����
����

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�����Ŀ��ijУ��֯ȫУѧ��������һ�������������ļ�ֵ����֪ʶ���������������ȡ�˸��꼶����ѧ���ɼ�����ͳ�ƣ���������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ�����ṩ����Ϣ������������⣺
�����Σ� | Ƶ�� | Ƶ�� |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
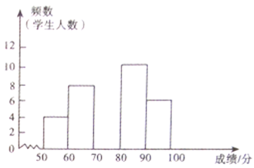
��1���������У�����ȡ��____ѧ���ɼ�����ͳ�ƣ�
��2������![]() ____��
____��![]() ____������ȫֱ��ͼ��
____������ȫֱ��ͼ��
��3����������ͳ��ͼ�����˳ɼ�ͳ�Ʒֲ�������������![]() ��Ӧ���ε�Բ�ĽǶ�����___
��Ӧ���ε�Բ�ĽǶ�����___![]() ��
��
��4������У����ѧ��8000�ˣ�����Ƹ�У������![]() ��ѧ���ж����ˣ�
��ѧ���ж����ˣ�