题目内容
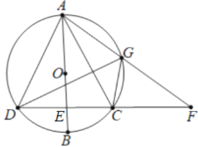
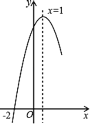
【题目】如图,已知抛物线![]() 经过点A(3,1)与点B(0,4).
经过点A(3,1)与点B(0,4).

(1)求该抛物线的解析式及顶点坐标;
(2)在第三象限内的抛物线上有一点P,使得PA⊥AB,求点P的坐标;
(3)若点C(![]() ,
,![]() )在该抛物线上,当
)在该抛物线上,当![]() ≤
≤![]() ≤3时,1≤
≤3时,1≤![]() ≤5,请确定
≤5,请确定![]() 的取值范围.
的取值范围.
【答案】(1) ![]() , 顶点坐标为(1,5); (2)点P的坐标为(-2,-4); (3)
, 顶点坐标为(1,5); (2)点P的坐标为(-2,-4); (3) ![]() 的取值范围是:-1≤
的取值范围是:-1≤![]() ≤1.
≤1.
【解析】
(1)将![]() 代入
代入![]() ,解关于b、c的二元一次方程组,得到解析式进而求出顶点坐标;
,解关于b、c的二元一次方程组,得到解析式进而求出顶点坐标;
(2)分别过B与点P作![]() 轴的平行线BD、PE,过点A作
轴的平行线BD、PE,过点A作![]() 轴的垂线交BD于D、交PE于点E,证出AE=PE,设点P的坐标为
轴的垂线交BD于D、交PE于点E,证出AE=PE,设点P的坐标为![]() ,分别用含m的代数式表示出AE和PE的长,进而求出点P的坐标;
,分别用含m的代数式表示出AE和PE的长,进而求出点P的坐标;
(3)根据题意,分别求出q的最大值与最小值,从而确定q的取值范围.
(1)将![]() 代入
代入![]() 得
得
![]()
解得![]()
∴![]() ,
,![]()
∴所求的抛物线的解析式为:![]() , 顶点坐标为(1,5)
, 顶点坐标为(1,5)
(2)如图,分别过B与点P作![]() 轴的平行线BD、PE,过点A作
轴的平行线BD、PE,过点A作![]() 轴的垂线交BD于D、交PE于点E
轴的垂线交BD于D、交PE于点E
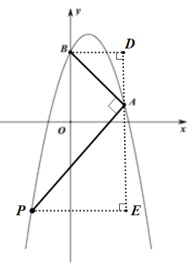
∵PA⊥AB
∴![]()
∴∠DAB+∠PAE=90°.
由A(3,1)、B(0,4)知BD=AD=3
∴∠DAB=45°
∴∠PAE=90°-∠DAB=90°-45°=45°
∴∠PAE=∠APE=45°
∴AE=PE
设点P的坐标为![]() 则
则
AE=![]()
PE=![]()
∴![]()
解得:![]() 或
或![]() (点P在第三象限,不合题意,舍去)
(点P在第三象限,不合题意,舍去)
∴![]() 时,
时,![]()
∴点P的坐标为(-2,-4).
(3)∵1≤n≤5且抛物线的顶点为(1,5)
∴区间包含顶点
∴![]() 的最大值为1
的最大值为1
在![]() 中,当
中,当![]() 时,
时,![]() 或者
或者![]()
∴![]() 的最小值为-1
的最小值为-1
∴![]() 的取值范围是:-1≤
的取值范围是:-1≤![]() ≤1.
≤1.

【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
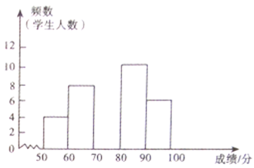
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?