题目内容
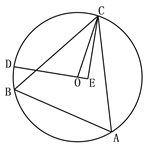
【题目】如图,△ABC为⊙O的内接三角形,BC=24 , ![]() ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
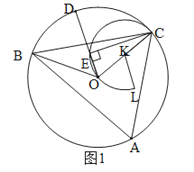
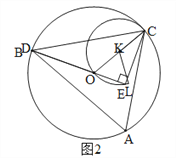
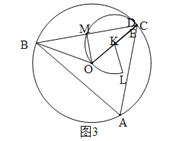
【解析】解:当点D由B点沿弧BC运动到点C时,点E经过的路径是以OC的中点K为圆心,以![]() OC为半径的一段圆弧,圆心角为240°,如图1.当D与B重合时,如图2,E和L重合.∵∠A=60°,∴∠BOC=120°,∴∠COE=60°.∵OK=KL,∴△OKL是等边三角形,∴∠OKL=60°.当D运动到C时,如图3,D、E、C三点重合,此时∠OKC=180°,∴∠LKC=60°+180°=240°.过O作OM⊥BC于M,如图3,则BM=
OC为半径的一段圆弧,圆心角为240°,如图1.当D与B重合时,如图2,E和L重合.∵∠A=60°,∴∠BOC=120°,∴∠COE=60°.∵OK=KL,∴△OKL是等边三角形,∴∠OKL=60°.当D运动到C时,如图3,D、E、C三点重合,此时∠OKC=180°,∴∠LKC=60°+180°=240°.过O作OM⊥BC于M,如图3,则BM=![]() BC=12.∵∠BOC=120°,OB=OC,∴∠MBO=(180°-120°)÷2=30°,∴OM=
BC=12.∵∠BOC=120°,OB=OC,∴∠MBO=(180°-120°)÷2=30°,∴OM=![]() ,OB=2OM=
,OB=2OM=![]() ,∴OK=
,∴OK=![]() OB=
OB=![]() ,∴点E经过的路径长为
,∴点E经过的路径长为![]() =
=![]() .故选C.
.故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目