题目内容
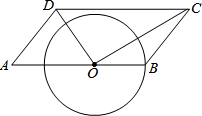
如图,平行四边ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P、Q.若OB=4,OD=6,∠ADO=∠A,
=2π,判断直线DC与⊙O的位置关系,并说明理由.
 |
| PQ |

如图,在⊙O中,半径OB=4,
设∠POQ为n°,则有
2π=
.
n=90°.
∴∠POQ=90°.
∵∠ADO=∠A,
∴AO=DO=6.
∴AB=10.
∵四边形ABCD是平行四边形,
∴DC=AB=10.
∴CO=8.
过点O作OE⊥CD于点E,
则OD×OC=OE×CD.
∴OE=4.8.
∵4.8>4,
∴直线DC与⊙O相离.

设∠POQ为n°,则有
2π=
| 8πn |
| 360 |
n=90°.
∴∠POQ=90°.
∵∠ADO=∠A,
∴AO=DO=6.
∴AB=10.
∵四边形ABCD是平行四边形,
∴DC=AB=10.
∴CO=8.
过点O作OE⊥CD于点E,
则OD×OC=OE×CD.
∴OE=4.8.
∵4.8>4,
∴直线DC与⊙O相离.

练习册系列答案
相关题目







