题目内容
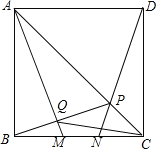
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为边
为边![]() 上一动点,作
上一动点,作![]() ⊥
⊥![]() ,垂足
,垂足![]() 在边
在边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径画圆,交射线
为半径画圆,交射线![]() 于点
于点![]() .
.
(1)当圆![]() 过点
过点![]() 时,求圆
时,求圆![]() 的半径;
的半径;
(2)分别联结![]() 和
和![]() ,当
,当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆
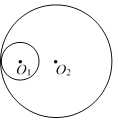
为半径的圆![]() 与圆
与圆![]() 相交,试求圆
相交,试求圆![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)将劣弧![]() 沿直线
沿直线![]() 翻折交
翻折交![]() 于点
于点![]() ,试通过计算说明线段
,试通过计算说明线段![]() 和
和![]() 的比值为定值,并求出次定值.
的比值为定值,并求出次定值.

【答案】(1)x=3 (2)![]() (3)
(3)![]()
【解析】
(1)作AM⊥BC、连接AP,由等腰梯形性质知BM=4、AM=3,据此知tanB=tanC=![]() ,从而可设PH=3k,则CH=4k、PC=5k,再表示出PA的长,根据PA=PH建立关于k的方程,解之可得;
,从而可设PH=3k,则CH=4k、PC=5k,再表示出PA的长,根据PA=PH建立关于k的方程,解之可得;
(2)由PH=PE=3k、CH=4k、PC=5k及BC=9知BE=98k,由△ABE∽△CEH得![]() ,据此求得k的值,从而得出圆P的半径,再根据两圆间的位置关系求解可得;
,据此求得k的值,从而得出圆P的半径,再根据两圆间的位置关系求解可得;
(3)在圆P上取点F关于EH的对称点G,连接EG,作PQ⊥EG、HN⊥BC,先证△EPQ≌△PHN得EQ=PN,由PH=3k、HC=4k、PC=5k知sinC=![]() 、cosC=
、cosC=![]() ,据此得出NC=
,据此得出NC=![]() k、HN=
k、HN=![]() k及PN=PCNC=
k及PN=PCNC=![]() k,继而表示出EF、EH的长,从而出答案.
k,继而表示出EF、EH的长,从而出答案.
(1)作AM⊥BC于点M,连接AP,如图1,

∵梯形ABCD中,AD//BC,且AB=DC=5、AD=1、BC=9,
∴BM=4、AM=3,
∴tanB=tanC=![]() ,
,
∵PH⊥DC,
∴设PH=3k,则CH=4k、PC=5k,
∵BC=9,
∴PM=BCBMPC=55k,
∴AP![]() =AM
=AM![]() +PM
+PM![]() =9+(55k)
=9+(55k) ![]() ,
,
∵PA=PH,
∴9+(55k) ![]() =9k
=9k![]() ,
,
解得:k=1或k=![]() ,
,
当k=![]() 时,CP=5k=
时,CP=5k=![]() >9,舍去;
>9,舍去;
∴k=1,
则圆P的半径为3.
(2)如图2,

由(1)知,PH=PE=3k、CH=4k、PC=5k,
∵BC=9,
∴BE=BCPEPC=98k,
∵△ABE∽△CEH,
∴![]() ,即
,即![]() ,
,
解得:k=![]() ,
,
则PH=![]() ,即圆P的半径为
,即圆P的半径为![]() ,
,
∵圆B与圆P相交,且BE=98k=![]() ,
,
∴![]() <r<
<r<![]() ;
;
(3)在圆P上取点F关于EH的对称点G,连接EG,作PQ⊥EG于G,HN⊥BC于N,

则EG=EF、∠1=∠3、EQ=QG、EF=EG=2EQ,
∴∠GEP=2∠1,
∵PE=PH,
∴∠1=∠2,
∴∠4=∠1+∠2=2∠1,
∴∠GEP=∠4,
∴△EPQ≌△PHN,
∴EQ=PN,
由(1)知PH=3k、HC=4k、PC=5k,
∴sinC=![]() 、cosC=
、cosC=![]() ,
,
∴NC=![]() k、HN=
k、HN=![]() k,
k,
∴PN=PCNC=![]() k,
k,
∴EF=EG=2EQ=2PN=![]() k,EH=
k,EH=![]() ,
,
∴![]() ,
,
故线段EH和EF的比值为定值.