题目内容
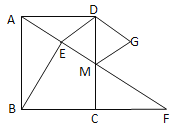
【题目】如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.

【答案】(1)详见解析;(2)![]()
【解析】
(1)由矩形性质得到∠B=∠DFA,AE=BC,AD=BC,证得△AEB≌△DAF;
(2)由(1)可知:DF=AB=6,AE=AD=10. 在Rt△AFD中,求出AF和EF.
(1)证明:在矩形ABCD中,AD=BC,AD∥BC,∠B=90°.
∵AD∥BC,
∴∠BEA=∠FAD
∵DF⊥AE,
∴∠DFA=90°
∴∠B=∠DFA
∵AE=BC,AD=BC,
∴AE=AD
∴△AEB≌△DAF
∴AB=DF
(2)解:由(1)可知:AB=DF=6,AE=AD=10.
在Rt△AFD中,∠DFA=90°,
∴AF=![]() =
=![]() =8
=8
∴EF=AE-AF=10-8=2
在Rt△DFE中,∠DFE=90°
∴tan∠EDF=![]() =
=![]() =
=![]()

练习册系列答案
相关题目