题目内容
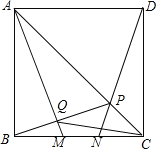
【题目】如图,M,N是正方形ABCD的边BC上两个动点,满足BM=CN,连结AC交DN于点P,连结AM交BP于点Q,若正方形的边长为1,则线段CQ的最小值是_____.
【答案】![]()
【解析】
首先证明点Q在以AB为直径的圆上运动,连接OC与 O交于点Q′,此时CQ′最小,根据勾股定理即可计算.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ACB=∠ACD=45°
在△ABM和△DCN中,
 ,
,
∴△ABM≌△DCN,
∴∠BAM=∠CDN,
在△CPB和△CPD中,
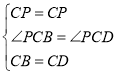 ,
,
∴△CPD≌△CPB,
∴∠CDP=∠CBP=∠BAM,
∵∠CBP+∠ABP=90°,
∴∠BAM+∠ABP=90°,
∴∠AQB=90°,
∴点Q在以AB为直径的圆上运动,设圆心为O,连接OC交⊙O于点Q′,此时CQ′最小,
∴CQ′=OC﹣OQ′=![]() .
.
故答案为![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目