题目内容
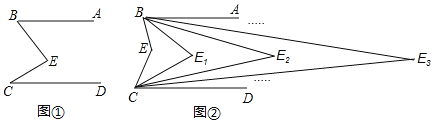
【题目】已知,如图,AB∥CD,分别探究下列四个图形(图①、②、③、④)中∠APC和∠PAB、∠PCD的数量关系,用等式表示出来.

(1)设∠APC=m,∠PAB=n,∠PCD=t.
请用含m,n,t的等式表示四个图形中相应的∠APC和∠PAB、∠PCD的数量关系.(直接写出结果)
图①: ;
图②: ;
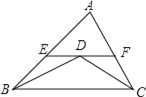
图③: ;
图④: .
(2)在(1)中的4个结论中选出一个你喜欢的结论加以证明.
【答案】(1)图①:m=n+t;图②:m+n+t=360°;图③:m+n=t;图④:m﹣t+n=180°(2)详见解析.
【解析】(1)依据∠APC=m,∠PAB=n,∠PCD=t,写出∠APC和∠PAB、∠PCD的数量关系即可.
(2)图①中,作PE∥AB;图②中,作PF∥AB;图③中运用三角形外角性质;图④中,作PH∥AB,分根据平行线的性质进行推导计算即可得出结论.
若选图①,过P作PE∥AB,则PE∥CD,
∴∠A=∠APE=n,∠C=∠CPE=t,
∴∠APC=∠APE+∠CPE=∠A+∠C,即m=n+t;
其他参考答案
若选图②,
过P作PF∥AB,则PF∥CD,
∴∠A+∠APF=180°,∠C+∠CPF=180°,
∴∠A+∠APF+∠C+∠CPF=180°×2=360°,
即∠A+∠APC+∠C=360°,∴m+n+t=360°;
若选图③,
∵AB∥CD,∴∠PGB=∠C,
又∵∠PGB=∠A+∠APC,
∴∠C=∠A+∠APC,即m+n=t;
若选图④,
过P作PH∥AB,则PH∥CD,
∴∠A+∠APH=180°,∠C=∠CPH=t,
又∵∠APH=∠APC﹣∠CPH=m﹣t,
∴n+m﹣t=180°.

练习册系列答案
相关题目