题目内容
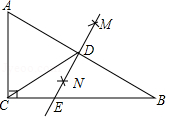
【题目】(题文)如图,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50![]() ,
,
求∠AOC,∠AOF,∠EOF的度数.

【答案】∠AOC=40 °,∠AOF=100 °,∠EOF=130°
【解析】根据题意即可推出∠EOD=90°,∠BOD=40°,既而得,∠AOC=40°,∠BOF=80°,得:∠EOF=130°,∠AOF=100°.
∵OE⊥CD于点O,
∴∠EOD=90°(垂直的定义) ,
∵∠BOE=50°,
∴∠BOD=90°-50°=40°,
∴∠AOC=∠BOD=40°(对顶角相等),
∵OD平分∠BOF,
∴∠BOF=2∠BOD=80°(角平分线的定义),
∴∠AOF=180°-80°=100°,(平角的定义).
∴∠EOF=∠EOB+∠BOF=130°.
答:∠AOC=40 °,∠AOF=100 °,∠EOF=130°.
点精:本题考查了垂线,角平分线的定义,对顶角、邻补角.

练习册系列答案
相关题目