题目内容
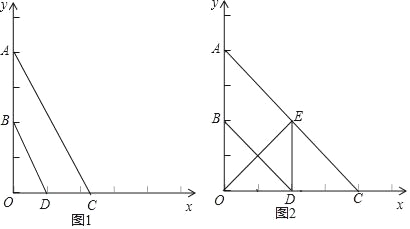
【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(![]() ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;
(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是![]() ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

【答案】(1)Q;(2)-![]() ;(3)(-4,
;(3)(-4,![]() ),(-
),(-![]() ,4);(4)8
,4);(4)8
【解析】
(1)根据“垂点”的意义直接判断即可得出结论;
(2)根据“垂点”的意义建立方程即可得出结论;
(3)根据“垂点”的意义和矩形的面积建立方程即可得出结论;
(4)先确定出直线EF的解析式,利用“垂点”的意义建立方程,利用非负性即可确定出m的范围,即可得出结论.
(1)∵P(1,2),∴1+2=3,1×2=2,
∵2≠3,∴点P不是“垂点”,
∵Q(2,﹣2),∴2+2=4,2×2=4,∴Q是“垂点”.
∵N(![]() ,﹣1),∴
,﹣1),∴![]() +1=
+1=![]() ×1=
×1=![]() ,
,
∵![]() ,∴点N不是“垂点”,
,∴点N不是“垂点”,
故答案为:Q;
(2)∵点 M(﹣4,m)是第三象限的“垂点”,∴4+(﹣m)=4×(﹣m),∴m=﹣![]() ,
,
故答案为:﹣![]() ;
;
(3)设“垂点”的坐标为(a,b),∴﹣a+b=﹣ab,
∵“垂点矩形”的面积为![]() ,∴﹣ab=
,∴﹣ab=![]() .
.
即:﹣a+b=﹣ab=![]() ,
,
解得:a=﹣4,b=![]() 或a=﹣
或a=﹣![]() ,b=4,∴“垂点”的坐标为(﹣4,
,b=4,∴“垂点”的坐标为(﹣4,![]() )或(﹣
)或(﹣![]() ,4),
,4),
故答案为:(﹣4,![]() )或(﹣
)或(﹣![]() ,4),.
,4),.
(4)设点E(m,0)(m>0),
∵四边形EFGH是正方形,∴F(0,m),y=﹣x+m.设边EF上的“垂点”的坐标为(a,﹣a+m),∴a+(﹣a+m)=a(﹣a+m)
∴a2﹣am=﹣m,∴(a﹣![]() )2=
)2=![]() ≥0,∴m2﹣4m=m(m﹣4)≥0,
≥0,∴m2﹣4m=m(m﹣4)≥0,
∵m>0,∴m﹣4≥0,∴m≥4,∴m的最小值为4,∴EG的最小值为2m=8,
故答案为:8.