题目内容
【题目】如图,四边形ABCD中,AB=AD=2,∠A=60°,BC=![]() ,CD=3.
,CD=3.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.

【答案】(1)150°; (2)![]()
【解析】试题分析:
(1)将△ABC绕点逆时针旋转60°,则有等边△ACC′,点D到等边△ACC′的距离符合勾股定理的逆定理,故将△ADC绕点A逆时针旋转60°,即可求解.
(2)将四边形ABCD分割为等边三角形和直角三角形,分别求出等边三角形和直角三角形的面积即可.
试题解析:
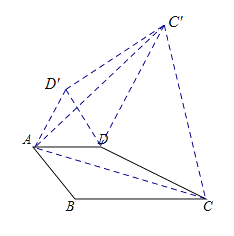
(1)如图,把△ABC绕点A逆时针旋转60°,构成三角形ACC′,把△ADC绕点A逆时针旋转60°,构成△AD′C.
由旋转的性质可知,△ACC′与△ADD′是等边三角形,且DC′=BC=![]() ,AD′=DD′=AD=2,D′C′=DC=3,∠AD′C=∠ADC.
,AD′=DD′=AD=2,D′C′=DC=3,∠AD′C=∠ADC.
因为DD′2=4,D′C′2=9,DC′2=13,所以DD′2+D′C′2=DC′2.
所以△DD′C′是直角三角形,所以∠DD′C′=90°,
因为∠AD′D=60°,所以∠AD′C=60°+90°=150°.
所以∠ADC=150°.
(2)由(1)知,S四边形ABCD=S四边形ADC′D′.
S四边形ADC′D′=S等边△ADD′+SRt△DD′C′=![]() =3+
=3+![]() .
.

练习册系列答案
相关题目


