题目内容
如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=_______.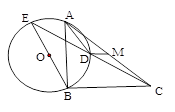

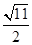
试题分析:连接AE、BD,先根据圆周角定理可得到∠EAB=∠EDB=90°,∠BAD=∠BED,即可得到∠BED=∠BCD,则BC=BE=6,根据勾股定理即可求得AE的长,再根据等腰三角形的性质可得点D为CE的中点,再由M为AC的中点根据三角形的中位线定理即可求得结果.
连接AE、BD
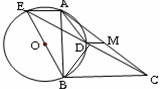
∵BE是⊙O的直径
∴∠EAB=∠EDB=90°,∠BAD=∠BED
∵∠BAD=∠BCD
∴∠BED=∠BCD
∴BC=BE=6
∴点D为CE的中点(等腰三角形三线合一)
∵AB=5
∴
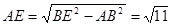
∵点D为CE的中点,点M为AC的中点
∴DM=
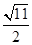 .
.点评:此类问题综合性强,难度较大,在中考中比较常见,题目比较典型.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 ,半径
,半径 ,则扇形的圆心角是 。
,则扇形的圆心角是 。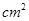 .
.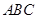 为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O 上,∠BAC=35°,则∠ADC= 度.
为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O 上,∠BAC=35°,则∠ADC= 度.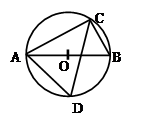
 的圆周角所对的弦是直径; ④不在同一条直线上的三个点确定一个圆;
的圆周角所对的弦是直径; ④不在同一条直线上的三个点确定一个圆;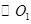 与
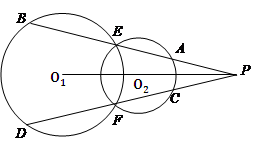
与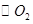 相交于点E、F,点P是两圆连心线上的一点,分别联结PE、PF交
相交于点E、F,点P是两圆连心线上的一点,分别联结PE、PF交