题目内容
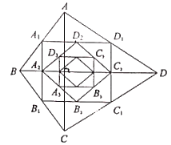
【题目】如图,四边形![]() 中,
中,![]() 顺次连接四边形
顺次连接四边形![]() 各边中点,得到四边形
各边中点,得到四边形![]() ,再顺次连接四边形
,再顺次连接四边形![]() 各边中点,得到四边形
各边中点,得到四边形![]() ...如此进行下去,得到四边形
...如此进行下去,得到四边形![]() 则下列结论正确的个数有( )
则下列结论正确的个数有( )
①四边形![]() 是矩形;②四边形
是矩形;②四边形![]() 是菱形;③四边形
是菱形;③四边形![]() 的周长为
的周长为![]() ; ④四边形
; ④四边形![]() 的面积是
的面积是![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】A
【解析】
首先根据题意,找出变化后的四边形的边长与四边形ABCD中各边长的长度关系规律,然后对以下选项作出分析与判断:
①根据矩形的判定与性质作出判断;
②根据菱形的判定与性质作出判断;
③由四边形的周长公式:周长=边长之和,来计算四边形A5B5C5D5的周长;
④根据四边形AnBnCnDn的面积与四边形ABCD的面积间的数量关系来求其面积.
解:如下图,连接连接A1C1,B1D1,
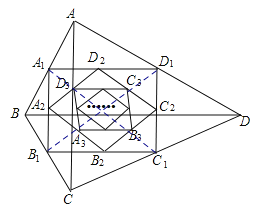
∵在四边形ABCD中,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形,
∵AC丄BD,
∴四边形A1B1C1D1是矩形,故①正确;
∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
依次类推,可知当n为奇数时四边形AnBnCnDn是矩形,当n为偶数时四边形AnBnCnDn是菱形,故②正确;
根据中位线的性质可知,![]() ,
,
∴四边形A5B5C5D5的周长是![]() ,
,
故③正确;
∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是![]() ,
,
故④正确;
综上所述,①②③④正确.
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目