题目内容
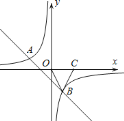
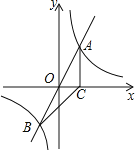
【题目】如图, 正比例函数![]() 的图象与反比例函数
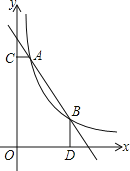
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
【答案】(1)k=2(2)D(![]() ,0)或(-
,0)或(-![]() ,0)
,0)
【解析】试题分析:(1)根据对称性可得OA=OB,从而可得△ACO的面积为1,由此可求出点A的坐标,然后运用待定系数法就可解决问题,
(2)先将y=2x与y=![]() 联立成方程组,求出A,B两点的坐标,由 O为线段AB的中点,
联立成方程组,求出A,B两点的坐标,由 O为线段AB的中点,
可得OD=![]() AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
试题解析:(1)设点A的坐标为(m,n),
∵点A在直线y=2x上,
∴n=2m,
根据对称性可得OA=OB,
∴S△ABC=2S△ACO=2,
∴S△ACO=1,
∴![]() m2m=1,
m2m=1,
∴m=1(舍负),
∴点A的坐标为(1,2),
∴k=1×2=2,
(2)x轴上存在一点D,使△ABD为直角三角形,
将y=2x与y=![]() 联立成方程组得:
联立成方程组得:
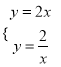 ,
,
解得: ![]() ,
,![]() ,
,
∴A(1,2),B(-1,-2),
当AD⊥BD时,如图,
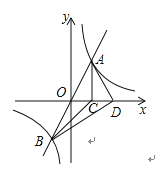
∵O为线段AB的中点,
∴OD=![]() AB=OA,
AB=OA,
∵A(1,2),
∴OC=1,AC=2,
由勾股定理得:OA=![]() =
=![]() ,
,
∴OD=![]() ,
,
∴D(![]() ,0),
,0),
根据对称性,当D为直角顶点,且D在x轴负半轴时,D(-![]() ,0),
,0),
故x轴上存在一点D,使△ABD为直角三角形,点D的坐标为(![]() ,0)或(-
,0)或(-![]() ,0).
,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目