题目内容
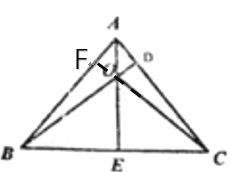
【题目】如图，△ABC中，BD⊥AC，AE⊥BC，AE、BD交于点O，连接CO，∠ABC=54°，∠ACB=48°，则∠COD=（ ）
A. 51°B. 66°C. 78°D. 88°
【答案】C
【解析】
延长CO与AB交于点F，利用三角形内角和定理和三角形三条高所在直线交于一点可求得∠COD=∠OBE+∠OCE=∠OAD+∠OAF=∠BAC=78°。
解：延长CO与AB交于点F.
∵三角形的三条高交于一点，BD⊥AC，AE⊥BC，
∴CF⊥AB
∵∠ABC=54°，∠ACB=48°，
∴∠BAC=78°
在△AOD和△BOE中, ∠AOD=∠BOE，∠OEB=∠ODA,
∴∠OBE=∠OAD,
同理，∠OAF=∠OCE,
∴∠COD=∠OBE+∠OCE=∠OAD+∠OAF=∠BAC=78°
故选：C
练习册系列答案
名师金手指领衔课时系列答案
相关题目
