��Ŀ����
����Ŀ����ѧ��ȤС�鿪չ��һ�ο������������£�
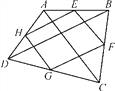
��ͼ�٣�������ABCD�У�AB=6�������ǰ����������ABCD�ϣ�ʹ���ǰ��ֱ�Ƕ�����D���غϣ����ǰ��һ�߽�AB�ڵ�P����һ�߽�BC���ӳ����ڵ�Q��

��1����֤��AP=CQ��
��2����ͼ�ڣ�С����ͼ�ٵĻ���������PDQ��ƽ����DE��BC�ڵ�E������PE��������PE��QE����һ����������ϵ����²����Ľ��۲�֤����
��3����ͼ�ۣ��̶����ǰ�ֱ�Ƕ�����D�㲻����ת�����ǰ壬ʹ���ǰ��һ�߽�AB���ӳ����ڵ�P����һ�߽�BC���ӳ����ڵ�Q��������PDQ��ƽ����DE��BC���ӳ����ڵ�E������PE����AB��AP=3��4�����С������� DEQ�������
���𰸡���1��֤������������2��PE=QE��֤������������3��![]()
��������������(1)��ASA֤����ADP�ա�CDQ��(2)��SAS֤����DEP�ա�DEQ��(3)��QE��PE��x����BE��14��x����Rt��BPE�У��ɹ��ɶ�����QE����S��DEQ���֡�DEP�ա�DEQ��������.
��⣺(1)֤�����ߡ�ADC����PDQ��90�������ADP����CDQ��
����ADP����CDQ����DAP����DCQ��90����AD��CD����ADP����CDQ��
���ADP�ա�CDQ(ASA)����AP��CQ��
(2)PE��QE��
֤������(1)��֪��ADP�ա�CDQ����DP��DQ��
��DEƽ�֡�PDQ�����PDE����QDE.
����DEP����DEQ��DP��DQ����PDE����QDE��DE��DE.
���DEP�ա�DEQ(SAS)��PE��QE��
(3)�⣺��AB��AP��3��4��AB��6����AP��8��BP��2��
��(1)ͬ��������֤����ADP�ա�CDQ����CQ��AP��8��
��(2)ͬ��������֤����DEP�ա�DEQ����PE��QE��
��QE��PE��x����BE��BC��CQ��QE��14��x��
��Rt��BPE�У��ɹ��ɶ����ã�
��ã�x��![]() ����QE��
����QE��![]() ��
��
��S��DEQ��![]() QECD��
QECD��![]() ��
��![]() ��6��
��6��![]() ��
��
�ߡ�DEP�ա�DEQ��
��S��DEP��S��DEQ��![]() ��
��

 53���ò�ϵ�д�
53���ò�ϵ�д�