��Ŀ����
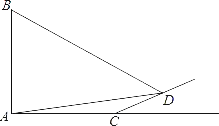
����Ŀ��Ϊ�������ܻ�����������Դ���ģ��ᳫ����������Դ�������츣��ᣮij��˾�з�����һ���������ܻ������ܵƣ��ɱ�Ϊÿ��40Ԫ���г����鷢�֣������ܻ������ܵ�ÿ���ۼ�y��Ԫ����ÿ���������Ϊx�������Ĺ�ϵ��ͼ��Ϊ�ƹ��²�Ʒ����˾Ҫ��ÿ���������������1000����ÿ��������5Ԫ��
��1����ÿ�����۵���y��Ԫ����ÿ���������Ϊx�������ĺ�����ϵʽ��ֱ��д���Ա���x��ȡֵ��Χ��
��2����ù�˾����������ΪPԪ����ÿ���������������Ƕ���Ԫ��
��3���������۹����У��ܹ������߷��֣�������һ�������ܻ������ܵƹ��Ҹ��蹫˾����m��m��40��Ԫ���ڻ�ù���ÿ��mԪ������˾�����������������������������������m��ȡֵ��Χ���� ����ֱ��д���������

���𰸡���1��������ϵʽΪy����![]() x+70���Ա���x��ȡֵ��Χ1000��x��2500����2��ÿ����������������22500Ԫ����3��m��ȡֵ��Χ�ǣ�20��m��40��
x+70���Ա���x��ȡֵ��Χ1000��x��2500����2��ÿ����������������22500Ԫ����3��m��ȡֵ��Χ�ǣ�20��m��40��
��������
��1�����ô���ϵ�������ɽ�����⣻
��2���������κ��������ö��κ��������ʼ��ɽ�����⣻
��3���������κ��������ö��κ��������ʼ��ɽ�����⣻
�⣺��1����ÿ�����۵���y��Ԫ����ÿ���������Ϊx�������ĺ�����ϵʽΪy��kx+b��
�ѣ�1500��55���루2000��50������y��kx+b�ã�
![]() ��
��
��ã�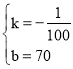 ��
��
��ÿ�����۵���y��Ԫ����ÿ���������Ϊx�������ĺ�����ϵʽΪy����![]() x+70��
x+70��
��y��45ʱ����![]() x+70��45����ã�x��2500��
x+70��45����ã�x��2500��
���Ա���x��ȡֵ��Χ1000��x��2500��
��2����������ã�P����y��40��x������![]() x+70��40��x����
x+70��40��x����![]() x2+30x����
x2+30x����![]() ��x��1500��2+22500��
��x��1500��2+22500��
����![]() ��0��P�����ֵ��
��0��P�����ֵ��
��x��1500ʱ��P��x�����������
����x��1500ʱ��P�����ֵΪ22500Ԫ��
��ÿ����������������22500Ԫ��
��3��������ã�P������![]() x+70��40+m��x����
x+70��40+m��x����![]() x2+��30+m��x��
x2+��30+m��x��
���Գ���Ϊx��50��30+m����
��1000��x��2500��
��x��ȡֵ��Χ�ڶԳ�������ʱP��x�����������
50��30+m����2500��
��ã�m��20��
��m��ȡֵ��Χ�ǣ�20��m��40��
�ʴ�Ϊ��20��m��40��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�