题目内容
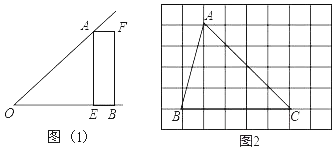
【题目】如图，等边三角形△ABC的边长为4，过点C的直线
⊥AC，且△ABC与△A′B′C关于直线对称，D为线段BC′上一动点，则AD+BD的最小值是______；
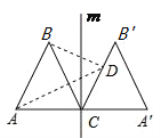
【答案】8
【解析】连接BB/，根据△ABC、△A/CB/均为正三角形即可得出A/CBB/为菱形，进而得出点B关于CB/对称的点A/，以此确定点D与点C重合时，AD+BD的最小，代入数据即可得出结论.
解：连接BB/，如图所示.
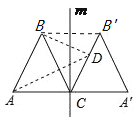
∵△ABC、△A/CB/ /均为正三角形，
∴∠ACB=∠A/=60°，A/C=BC=A/B/，
∴A/B/∥BC，
∴四边形A/CBB/ /为菱形，
∴点B关于CB/对称的点A/，
∴当点D与点C重合时，AD+BD取最小值，
此时AD+BD=4+4=8.
故答案为：8.
“点睛”本题考查了轴对称中的最短线路问题以及等边三角形的性质，找出点B关于CB/对称的点A/是解题的关键.
练习册系列答案
相关题目
【题目】某公司仓库本周内货物进出的吨数记录如下
“
”表示进库，“
”表示出库
；
日期 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
吨数 |
|
|
|
|
|
|
|
这一周，仓库内货物的总吨数是______了填“增多”或“减少”；
若周六结束时仓库内还有货物360吨，则周日开始时仓库内有货物多少吨？
如果该仓库货物进出的装卸费都是每吨5元，那么这一周内共需付多少元的装卸费？
