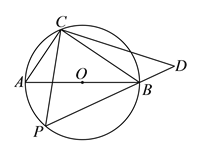
题目内容
【题目】如图,圆![]() 的直径为
的直径为![]() ,在圆
,在圆![]() 上位于直径
上位于直径![]() 的异侧有定点
的异侧有定点![]() 和动点
和动点![]() ,已知
,已知![]() ,点
,点![]() 在半圆弧
在半圆弧![]() 上运动(不与
上运动(不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 的延长线于
的延长线于![]() 点.
点.
(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 运动到
运动到![]() 弧中点时,求
弧中点时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到什么位置时,
运动到什么位置时, ![]() 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积![]() .
.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )
)![]() ;(
;(![]() )
)![]() 为直径时最大,
为直径时最大, ![]() 最大值=
最大值=![]() .
.
【解析】试题分析:(1)由圆周角定理知∠CAB=∠CPD,而∠ACB=∠PCD=90°,即可判定△ABC∽△PCD,根据相似三角形的性质可得![]() ,即可得结论;(2)当点P运动到AB弧中点时,过点B作BE⊥PC于点E.由题意知∠PCB=45°,CE=BE,而又∠CAB=∠CPB,得tan∠CPB=tan∠CAB=
,即可得结论;(2)当点P运动到AB弧中点时,过点B作BE⊥PC于点E.由题意知∠PCB=45°,CE=BE,而又∠CAB=∠CPB,得tan∠CPB=tan∠CAB=![]() ,代入数值可求得PE的值,从而求得PC的值,由(1)知CD=
,代入数值可求得PE的值,从而求得PC的值,由(1)知CD=![]() PC,即可求得CD的长;(3)由题意知,S△PCD=
PC,即可求得CD的长;(3)由题意知,S△PCD=![]() PCCD.由(1)可知,CD=
PCCD.由(1)可知,CD=![]() PC即可得S△PCD=
PC即可得S△PCD=![]() PC2.故PC最大时,S△PCD取得最大值;而PC为直径时最大,即可求解.
PC2.故PC最大时,S△PCD取得最大值;而PC为直径时最大,即可求解.
试题解析:
(![]() )∵
)∵![]() 为直径,
为直径,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )当
)当![]() 运动到
运动到![]() 中点时,过
中点时,过![]() 作
作![]() 于点
于点![]() ,
,
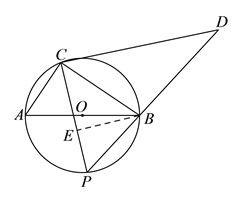
∵![]() 为直径,
为直径, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
∴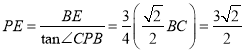 ,
,
从而![]() ,
,
由(![]() )得
)得![]() .
.
(![]() )当点
)当点![]() 在
在![]() 上运动时,
上运动时,
![]() ,由(
,由(![]() )得
)得![]() ,
,
∴![]() ,
,
故![]() 最大时,
最大时, ![]() 取得最大值.
取得最大值.
而![]() 为直径时最大,
为直径时最大,
∴![]() 最大值
最大值![]() .
.

练习册系列答案
相关题目