题目内容
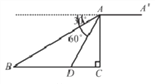
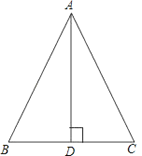
【题目】请你画出一个以BC为底边的等腰ΔABC，使底边上的高AD=BC．
（1）求tanB和 sinB的值；
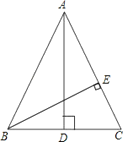
（2）在你所画的等腰ΔABC中设底边BC=5米，求腰上的高BE．
【答案】如图，正确画出图形，
（1）∵AB=AC，AD⊥BC，AD=BC，
∴BD=
BC=AD．即AD=2BD．
∴AB=
BD．
∴tanB=
，
sinB=
．
（2）在Rt△BEC中，sinC=sin∠ABC=
，
又∵sinC=
，
∴
．
故
（米）．
【解析】（1）本题可根据三角形的特殊性（等腰三角形）和AD=BC，先求出AD和BD，CD的关系，进而求出tan B和sinB的值；
（2）由于是等腰三角形，∠B=∠C，求出了sinB也就是求出了sinC，直角三角形BCE中，已知了BC的长，BE就不难求出了．
练习册系列答案
春雨教育同步作文系列答案
相关题目
【题目】探究函数
的图象与性质，下面是探究过程，请补充完整：
（
）下表是
与
的几组对应值．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
函数
的自变量
的取值范围是__________， 
的值为__________．
（
）描出以上表中各对对应值为坐标的点，并画出该函数的大致图象．
（
）进一步探究函数图象发现：
①函数图象与
轴有__________个交点，所以对应方程
有__________个实数根．
②方程
有__________个实数根．
③结合函数的图象，写出该函数的一条性质__________．
