Question

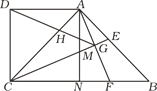
【题目】如图，正方形中，，，交于点．若，分别是边，上的动点，且，则周长的最小值是__________．

Answer 1

【答案】

【解析】

根据正方形的对角线互相平分且相等可得AO=BO，∠AOB=90°，对角线平分一组对角可得∠OAE=∠OBF，再根据AE=BF，然后利用“SAS”证明△AOE和△BOF全等，根据全等三角形对应角相等可得∠AOE=∠BOF，可得∠EOF=90°，然后利用勾股定理列式计算即可得解．

解：在正方形ABCD中，AO=BO，∠AOB=90°，∠OAE=∠OBF=45°，

∵点E、F的速度相等，

∴AE=BF，

在△AOE和△BOF中，

，

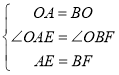∴△AOE≌△BOF（SAS），

∴∠AOE=∠BOF，

∴∠AOE+∠BOE=90°，

∴∠BOF+∠BOE=90°，

∴∠EOF=90°，

在Rt△BEF中，设AE=x，则BF=x，BE=2-x，

EF=．

∴当x=1时，EF有最小值为．

∴OE=OF=1．

∴△OEF周长的最小值=．
故答案为：．