题目内容
【题目】已知y关于x的一次函数y=(2m2﹣32)x3﹣(n﹣3)x2+(m﹣n)x+m+n.
(1)若该一次函数的y值随x的值的增大而增大,求该一次函数的表达式,并在如图所示的平面直角坐标系中画出该一次函数的图象;
(2)若该一次函数的图象经过点(﹣2,13),求该函数的图象与坐标轴围成的三角形的面积.
【答案】
(1)解:∵y关于x的一次函数y=(2m2﹣32)x3﹣(n﹣3)x2+(m﹣n)x+m+n,
∴2m2﹣32=0,n﹣3=0,
解得:m=±4,n=3,
又∵该一次函数的y值随x的值的增大而增大,
∴m﹣n>0,
则m=4,n=3,
∴该一次函数的表达式为:y=x+7,
如图所示:
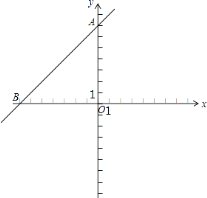
(2)解:∵该一次函数的图象经过点(﹣2,13),
∴y=﹣7x﹣1,
如图所示:
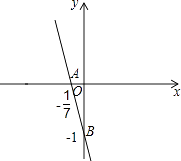 ,
,
当x=0,则y=﹣1,当y=0,则x=﹣ ![]() ,
,
故该函数的图象与坐标轴围成的三角形的面积为: ![]() ×1×
×1× ![]() =
= ![]()
【解析】(1)直接利用一次函数增减性结合一次函数的定义得出m,n的值进而画出图象;(2)利用一次函数图象上点的坐标特征得出一次函数解析式,进而求出图象与坐标轴围成的三角形的面积.
【考点精析】通过灵活运用一次函数的性质和确定一次函数的表达式,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目