题目内容
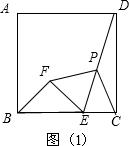
如图，在正方形ABCD中，E是BC的中点，F是CD上的一点，AE⊥EF，则下列结论正确的是（ ）
| A．∠BAE=30° | B．△ABE≌△AEF | C．CE2=AB•CF | D．CF=
|
因为∠BAE+∠BEA=90°，∠BEA+∠CEF=90°；
所以∠BAE=∠CEF，又因为∠B=∠C=90°，
所以△ABE∽△ECF
则AB：BE=EC：CF，
因为BE=CE，
所以AB：CE=EC：CF，
即CE2=AB•CF，
故答案为C．
所以∠BAE=∠CEF，又因为∠B=∠C=90°，
所以△ABE∽△ECF
则AB：BE=EC：CF，
因为BE=CE，
所以AB：CE=EC：CF，
即CE2=AB•CF，
故答案为C．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
分别为S1、S2、…S8，试比较S3与S2+S7+S8的大小，并说明理由．
构造一个与上述命题类似的正确命题并加以证明．
