Question

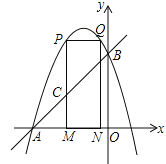
【题目】如图，在矩形ABCD中，AD＝4，∠BAC＝30°，点O为对角线AC上的动点（不与A、C重合），以点O为圆心在AC下方作半径为2的半圆O，交AC于点E、F．

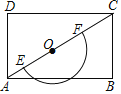
（1）当半圆O过点A时，求半圆O被AB边所截得的弓形的面积；

（2）若M为的中点，在半圆O移动的过程中，求BM的最小值；

（3）当半圆O与矩形ABCD的边相切时，求AE的长．

Answer 1

【答案】（1）π﹣；（2）2﹣1；（3）2或7﹣．

【解析】

（1）设半圆O与AB交于H，过点O作ON⊥AB于N，由直角三角形的性质和等腰三角形的性质可求AN＝NH＝2，∠AOH＝2∠AON＝120°，由扇形面积公式和三角形面积公式可求解；

（2）过点B作BP⊥AC于P，由题意可得点M在平行于AC且与AC的距离为1的直线上，则当点M在BF上时，BM有最小值，即可求解；

（3）分两种情况讨论，由直角三角形的性质可求解．

（1）如图1，设半圆O与AB交于H，过点O作ON⊥AB于N，

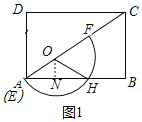
∵AO＝2，∠BAC＝30°，ON⊥AB，

∴ON＝1，AN＝ON＝，∠AON＝60°，

∵OA＝OH，ON⊥AB，

∴AN＝NH＝2，∠AOH＝2∠AON＝120°，

∴半圆O被AB边所截得的弓形的面积＝﹣×2×1＝π﹣；

（2）如图2，过点B作BP⊥AC于P，

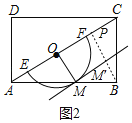
∵BC＝AD＝4，∠BAC＝30°，

∴AB＝BC＝4，AC＝2BC＝8，

∵BF⊥AC，∠BAC＝30°，

∴BF＝AB＝2，

∵M为的中点，

∴OM⊥AC，OM＝1，

∴点M在平行于AC且与AC的距离为1的直线上，

∴当点M在BF上时，BM有最小值，即最小值＝2﹣1；

（3）如图，当半圆O与AB相切于点G，连接OG，

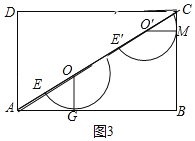
∴OG⊥AB，OG＝2，

∵∠CAB＝30°，

∴AO＝2OG＝4，

∴AE＝AO﹣OE＝4﹣2＝2；

当半圆O'与BC相切于点M，连接O'M，

∴O'M⊥BC，

∴O'M∥AB，

∴∠CO'M＝∠CAB＝30°，

∴O'C＝2×＝，

∴AE'＝8﹣1﹣＝7﹣，

综上所述：AE的长为2或7﹣．