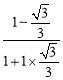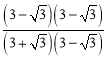题目内容
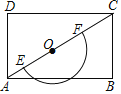
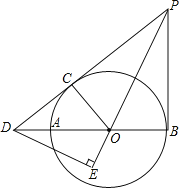
【题目】如图,AB是⊙O的直径,点C、E位于⊙O上AB两侧.在BA的延长线上取点D,使∠ACD=∠B.
(1)求证:DC是⊙O的切线;
(2)当BC=EC时,求证:AC2=AEAD;
(3)在(2)的条件下,若BC=4![]() ,AD:AE=5:9,求⊙O的半径.
,AD:AE=5:9,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OC,证明∠DCO=90°即可.
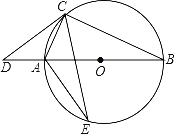
(2)连接BE.证明△ACD∽△AEC可得结论.
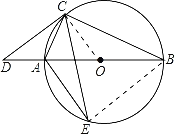
(3)设AD=5k,AE=9k,则AC=3![]() k,由△ACD∽△AEC,可得
k,由△ACD∽△AEC,可得![]() =
=![]() ,推出CD=
,推出CD=![]() ,由△DCA∽△DBC,可得CD2=DADB,推出DB=
,由△DCA∽△DBC,可得CD2=DADB,推出DB=![]() ,推出AB=
,推出AB=![]() ﹣5k,根据AC2+BC2=AB2,构建方程求出k即可解决问题.
﹣5k,根据AC2+BC2=AB2,构建方程求出k即可解决问题.
(1)证明:连接OC.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠ACO+∠B=90°,
又∵∠ACD=∠B,
∴∠ACD+∠ACO=90°,
∴∠DCO=90°,
∴DC是⊙O的切线;
(2)解:连接BE.
∵BC=EC,
∴![]() ,
,
∴∠CAB=∠CBE,
∵四边形CAEB内接于圆,
∴∠CBE+∠CAE=180°,
又∵∠CAD+∠CAB=180°,
∴∠CAD=∠CAE,
又∵∠ACD=∠B,∠B=∠AEC,
∴∠ACD=∠AEC,
∴△ACD∽△AEC,
∴![]() .
.
∴AC2=AEAD;
(3)解:设AD=5k,AE=9k,则AC=3![]() k,
k,
∵△ACD∽△AEC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴CD=![]() ,
,
∵∠D=∠D,∠ACD=∠CBD,
∴△DCA∽△DBC,
∴CD2=DADB,
∵DB=![]() ,
,
∴AB=![]() ﹣5k,
﹣5k,
∵∠ACB=90°,
∴AC2+BC2=AB2,
∴(3![]() k)2+(4
k)2+(4![]() )2=(
)2=(![]() )2,
)2,
整理得:81k4+684k2﹣320=0,
∴(9k2+80)(9k2﹣4)=0,
∴k2=![]() ,
,
∵k>0,
∴k=![]() ,
,
∴AB=![]() ,
,
∴⊙O的半径为![]() .
.

【题目】由于新冠肺炎影响,全国开展了“停课不停学”线上教学,为了解学生在家学习情况,五月7日开学后,某中学1200名学生参加了入学摸底测试,为了了解本次测试成绩情况,王老师从中抽取了部分学生的数学成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
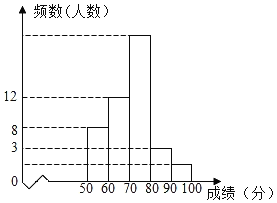
(1)写出a,b,c的值;
(2)请估计这1200名学生中有多少人的成绩不低于70分;
(3)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取两名同学参加学习经验分享活动,求所抽取的2名同学来自同一组的概率.