题目内容
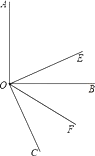
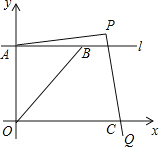
【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)当动点P在直线OB上时,点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,求PA:PC的值.
【答案】(1)PA的长为2;(2)PA:PC的值为1:1;(3)PA:PC的值为![]() 或
或![]() .
.
【解析】试题分析:(1)B点到y轴的距离是2.(2)过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,证明△ANP≌△CMP,可得PA:PC的值为1:1.(3)分类讨论,
若点P在线段OB的延长线上,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F,△ANP∽△CMP,证明四边形PMON是矩形,求出PA:PC值,若点P在线段OB的反向延长线上,,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F,同理求出比值.
试题解析:
(1)∵点P与点B重合,点B的坐标是(2,1),
∴点P的坐标是(2,1).
∴PA的长为2.
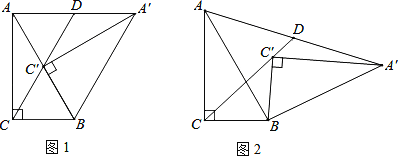
(2)如答图1,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,
∵点A的纵坐标与点B的横坐标相等,∴OA=AB.
∵∠OAB=90°,∴∠AOB=∠ABO=45°.
∵∠AOC=90°,∴∠POC=45°.
∵PM⊥x轴,PN⊥y轴,∴PM=PN,∠ANP=∠CMP=90°.∴∠NPM=90°.
∵∠APC=90°.∴∠APN=90°∠APM=∠CPM.
在△ANP和△CMP中,∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP,
∴△ANP≌△CMP.∴PA=PC.∴PA:PC的值为1:1.
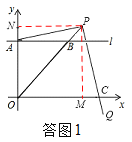
(3)①若点P在线段OB的延长线上,如答图2,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F.
∵∠APN=∠CPM,∠ANP=∠CMP,∴△ANP∽△CMP.∴ ![]() .
.
∵∠ACE=∠AEC,∴AC=AE.
∵AP⊥PC,∴EP=CP.
∵PM∥y轴,∴AF=CF,OM=CM.∴FM= ![]() OA.
OA.
设OA=x,∵PF∥OA,∴△PDF∽△ODA.∴ ![]() .
.
∵PD=2OD,∴PF=2OA=2x,FM= ![]() x.∴PM=
x.∴PM= ![]() x.
x.
∵∠APC=90°,AF=CF,∴AC=2PF=4x.
∵∠AOC=90°,∴OC= ![]() x.
x.
∵∠PNO=∠NOM=∠OMP=90°,∴四边形PMON是矩形.∴PN=OM= ![]() x.
x.
∴PA:PC=PN:PM= ![]() x:
x: ![]() x=
x= ![]() .
.
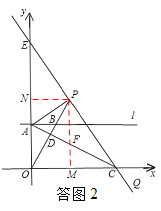
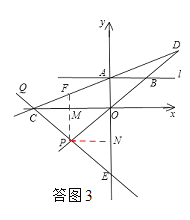
②若点P在线段OB的反向延长线上,如答图3,过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,PM与直线AC的交点为F.
同理可得:PM= ![]() x,CA=2PF=4x,OC=
x,CA=2PF=4x,OC= ![]() x.
x.
∴PN=OM= ![]() OC=
OC= ![]() x.
x.
∴PA:PC=PN:PM= ![]() x:
x: ![]() x=
x= ![]() .
.
综上所述:PA:PC的值为![]() 或
或 ![]() .
.

 名校课堂系列答案
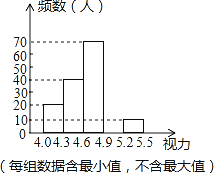
名校课堂系列答案【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?