题目内容
【题目】已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
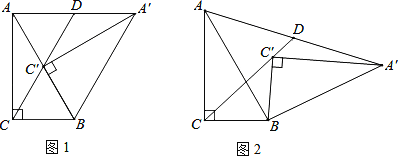
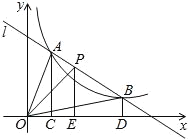
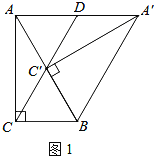
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
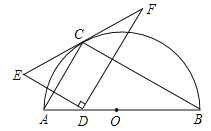
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
【答案】(1)AD=A′D,(2)仍然成立:AD=A′D(3)60°
【解析】
试题分析:(1)易证△BCC′和△BAA′都是等边三角形,从而可以求出∠AC′D=∠BAD=60°,∠DC′A′=∠DA′C′=30°,进而可以证到AD=DC′=A′D.
(2)解答中提供了两种方法,分别利用相似与全等,证明所得的结论.
(3)当A、C′、A′三点在一条直线上时,有∠AC′B=90°,易证Rt△ACB≌Rt△AC′B (HL),从而可以求出旋转角α的度数.
试题解析:答:(1)AD=A′D.
证明:如图1,
∵Rt△A′BC′≌Rt△ABC,
∴BC=BC′,BA=BA′.
∵∠A′BC′=∠ABC=60°,
∴△BCC′和△BAA′都是等边三角形.
∴∠BAA′=∠BC′C=60°.
∵∠A′C′B=90°,
∴∠DC′A′=30°.
∵∠AC′D=∠BC′C=60°,
∴∠ADC′=60°.
∴∠DA′C′=30°.
∴∠DAC′=∠DC′A,∠DC′A′=∠DA′C′.
∴AD=DC′,DC′=DA′.
∴AD=A′D.
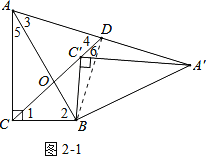
(2)仍然成立:AD=A′D.
证法一:利用相似.如图2﹣1.
由旋转可得,BA=BA′,BC=BC′,∠CBC′=∠ABA′
∵∠1=![]() (180°﹣∠ABA′),∠3=
(180°﹣∠ABA′),∠3=![]() (180°﹣∠CBC′)
(180°﹣∠CBC′)
∴∠1=∠3.
设AB、CD交于点O,则∠AOD=∠BOC
∴△BOC∽△DOA.
∴∠2=∠4,![]() .
.
连接BD,
∵∠BOD=∠COA,
∴△BOD∽△COA.
∴∠5=∠6.
∵∠ACB=90°,
∴∠2+∠5=90°.
∴∠4+∠6=90°,即∠ADB=90°.
∵BA=BA′,∠ADB=90°,
∴AD=A′D.
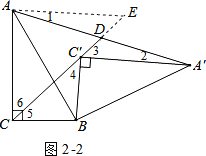
证法二:利用全等.如图2﹣2.
过点A作AE∥A′C′,交CD的延长线于点E,则∠1=∠2,∠E=∠3.
由旋转可得,AC=A′C′,BC=BC′,
∴∠4=∠5.
∵∠ACB=∠A′C′B=90°,
∴∠5+∠6=∠3+∠4=90°,
∴∠3=∠6.
∴∠E=∠6,∴AE=AC=A′C′.
在△ADE与△A′DC′中,

∴△ADE≌△A′DC′(ASA),
∴AD=A′D.
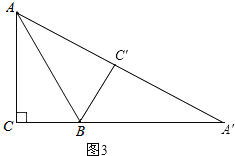
(3)当A、C′、A′三点在一条直线上时,如图3,
则有∠AC′B=180°﹣∠A′C′B=90°.
在Rt△ACB和Rt△AC′B中,
![]() .
.
∴Rt△ACB≌Rt△AC′B (HL).
∴∠ABC=∠ABC′=60°.
∴当A、C′、A′三点在一条直线上时,旋转角α的度数为60°.

【题目】下面为某年11月的日历:
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)在日历上任意圈出一个竖列上相邻的3个数;
①设中间的一个数为![]() ,则另外的两个数为 、 ;
,则另外的两个数为 、 ;
②若已知这三个数的和为42,则这三天都在星期 ;
(2)在日历上用一个小正方形任意圈出其中的9个数,设圈出的9个数的中心的数为b,若这9个数的和为153,求![]() 的值.
的值.