Question

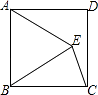
【题目】如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D为边AB上一点，CD绕点D顺时针旋转90°至DE，CE交AB于点G．已知AD＝8，BG＝6，点F是AE的中点，连接DF，求线段DF的长___．

Answer 1

【答案】

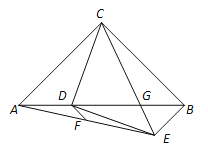
【解析】如图，将△ACD绕点C逆时针旋转90°得到△CBP，作CM⊥AB于M，EN⊥AB于N，在NA上截取一点H，使得NH=NE，连接HE，PG．

∵AC=BC，∠ACB=90°，

∴∠CAB=∠CBA=45°，

∵DC=DE，∠CDE=90°，

∴∠DCE=45°，

∴∠ACD+∠BCG=45°，

∵∠ACD=∠BCP，

∴∠GCP=∠GCD=45°，

在△GCD和△GCP中，

，

∴△GCD≌△GCP，

∴DG=PG，

∵∠PBG=∠PBC+∠CBG=90°，BG=6，PB=AD=8，

，

∴AB=AD+DG+BG=24，CM=AM=MB=12，DM=AM﹣AD=4，

∵∠DCM+∠CDM=90°，∠CDM+∠EDN=90°，

∴∠DCM=∠EDN，

在△CDM和△DEN中，，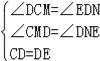

∴△CDM≌△DEN，

∴DM=NE=HN=4，CM=DN=AM，

∴AD=NM，DH=AD，

∵AF=FE，

．