题目内容
【题目】如图，四边形ABCD是正方形，△ABE是等边三角形，EC= 
，则正方形ABCD的面积为 ． 
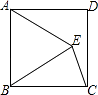
【答案】8
【解析】解：过点E作MN∥AD，交AB于点M，交CD于点N，如图所示．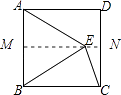 
设正方形的边长为a，则ME= 
a，NC= 
a，EN=AD﹣ME=a﹣ a，
在Rt△ENC中，由勾股定理得：
EC2=NC2+EN2 ， 即 
= 
+ 
，
解得：a2=8．
所以答案是：8．
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
相关题目
【题目】6月5日是世界环境日，为了普及环保知识，增强环保意识，某市第一中学举行了“环保知识竞赛”，参赛人数1000人，为了了解本次竞赛的成绩情况，学校团委从中抽取部分学生的成绩（满分为100分，得分取整数）进行统计，并绘制出不完整的频率分布表和不完整的频数分布直方图如下：
(1)直接写出a的值，并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5～59.5 | 0.08 | |
59.5～69.5 | 0.12 | |
69.5～79.5 | 20 | |
79.5～89.5 | 32 | |
89.5～100.5 | a |
(2)若成绩在80分以上（含80分）为优秀，求这次参赛的学生中成绩为优秀的约为多少人？
(3)若这组被抽查的学生成绩的中位数是80分，请直接写出被抽查的学生中得分为80分的至少有多少人？
