题目内容
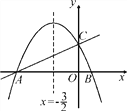
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-![]() ,且经过A,C两点,与x轴的另一交点为点B.
,且经过A,C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线的解析式.
(2)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)①点B的坐标为(1,0);②y=-![]() x2-
x2-![]() x+2;(2)存在点M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A,M,N为顶点的三角形与△ABC相似.
x+2;(2)存在点M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A,M,N为顶点的三角形与△ABC相似.
【解析】【试题分析】(1)①先求的直线y=![]() x+2与x轴、y轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;(3)证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC;③当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
x+2与x轴、y轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;(3)证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC;③当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
试题解析:
(1)①对于直线y=![]() x+2,当x=0时,y=2;当y=0时,x=-4,
x+2,当x=0时,y=2;当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于直线x=-![]() 对称,
对称,
∴点B的坐标为(1,0);
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a,
∴a=-![]() ,
,
∴y=-![]() x2-
x2-![]() x+2
x+2
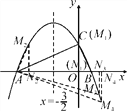
(2)在Rt△AOC中,易知△ABC∽△ACO∽△CBO,
如图,①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;
②根据抛物线的对称性,当M(-3,2)时,△MAN∽△ABC;
③当点M在第四象限时,设M(n,-![]() n2-
n2-![]() n+2),则N(n,0),
n+2),则N(n,0),
∴MN=![]() n2+
n2+![]() n-2,AN=n+4,
n-2,AN=n+4,
当![]() =
=![]() 时,MN=
时,MN=![]() AN,即
AN,即![]() n2+
n2+![]() n-2=
n-2=![]() (n+4),
(n+4),
整理得n2+2n-8=0,解得n1=-4(舍),n2=2,
∴M(2,-3);
当![]() =
=![]() 时,MN=2AN,即
时,MN=2AN,即![]() n2+
n2+![]() n-2=2(n+4),
n-2=2(n+4),
整理得n2-n-20=0解得n1=-4(舍),n2=5,
∴M(5,-18).
综上所述,存在点M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A,M,N为顶点的三角形与△ABC相似.

【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?