��Ŀ����
����Ŀ���Ķ�������ϣ�
��A��B�������Ϸֱ��ʾʵ��a��b��A��B����֮��ľ����ʾΪ�OAB�O.
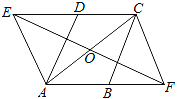
��A��B��������һ����ԭ��ʱ���������A��ԭ�㣬��ͼ1���OAB�O���OOB�O���Ob�O���Oa-b�O��
![]()
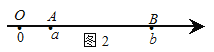
��A��B���㶼����ԭ��ʱ����ͼ2����A��B����ԭ����ұ�
�OAB�O=�OOB�O-�OOA�O=�Ob�O-�Oa�O=![]() =�Oa-b�O��
=�Oa-b�O��
��ͼ3������A��B����ԭ�����ߣ�
�OAB�O���OOB�O-�OOA�O���Ob�O-�Oa�O=![]() =�Oa-b�O��
=�Oa-b�O��
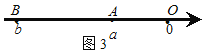
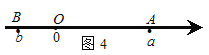
��ͼ4������A��B��ԭ������ߣ�
�OAB�O���OOB�O+�OOA�O���Oa�O+�Ob�O= ![]() =�Oa-b�O��
=�Oa-b�O��
�ش��������⣺
��1�������ϱ�ʾ1��6������֮��ľ����� �������ϱ�ʾ2�ͣ�3������֮��ľ����� ��
��2������������A��ʾ������x����B��ʾ�����ǣ�4�����A��B֮��ľ����� �����OAB�O��3����ôxΪ ��
��3����x�� ʱ������ʽ![]() ��
��
��4������A��ʾ����![]() ����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��
����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��![]() ����λ���ȣ����˶������Q���P ���1����λ������д����Ҫ�������̣�
����λ���ȣ����˶������Q���P ���1����λ������д����Ҫ�������̣�
���𰸡���1��5 ��5��2��![]() ��-7��-1��3��-4��3��4��
��-7��-1��3��-4��3��4��![]() ��
��![]()
�����������������
��1�����Ķ��������ݿ�֪������������������A��B����ʾ�����ֱ�Ϊ��a��b����A��B�����ľ���![]() ���ɴ˿ɼ��㱾��𰸣�
���ɴ˿ɼ��㱾��𰸣�
��2��ͬ��1���ɽ�õ�һ�յĴ������ݣ�1���еĹ�ʽ�;���ֵ�����壬���з��̽�õڶ��յĴ𰸣�
��3�����Ķ����Ͽ�֪��![]() ��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7�����Ƿ�
��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7�����Ƿ�![]() ��
��![]() ��
��![]() �������������ʽ��
�������������ʽ��![]() �Ϳ������x����ֵ��
�Ϳ������x����ֵ��
��4���������֪����A��ʾ����Ϊ��-1������B��ʾ�����ǡ�9����������֪�ɵã�![]() ��
��![]() ����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P���������������ۣ���ͼ1��ͼ2���г����̿���⣻
����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P���������������ۣ���ͼ1��ͼ2���г����̿���⣻
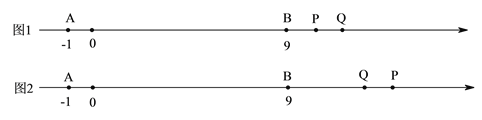
���������
��1����![]() ��
��
�����ն�Ӧ�5����
��2��������������A��ʾ������x����B��ʾ�����ǣ�4��
��![]() ��
��
����![]() ��
��
��![]() ����
����![]() �������
�������![]() ��
��![]() ��
��
��3�����Ķ����Ͽ�֪��![]() ��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7������Ҫ���Ƿ�
��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7������Ҫ���Ƿ�![]() ��
��![]() ��
��![]() ������������ۣ�
������������ۣ�
�ٵ�![]() ʱ��
ʱ��![]() �ɻ�Ϊ��
�ɻ�Ϊ��![]() ����ã�
����ã�![]() ��
��
����![]() ʱ��
ʱ��![]() �ɻ�Ϊ��
�ɻ�Ϊ��![]() ����ʽ�Ӳ�������
����ʽ�Ӳ�������
����![]() ʱ��
ʱ��![]() �ɻ�Ϊ��
�ɻ�Ϊ��![]() ����ã�
����ã�![]() ��
��
����������![]() ��
��![]() ��
��
��4���������֪����A��ʾ����Ϊ��-1������B��ʾ�����ǡ�9����������֪�ɵã�
![]() ��
��![]() ����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P������������������
����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P������������������
����ͼ1����Q��P���ұ�ʱ����![]() �ɵ���
�ɵ���![]() ����
����![]() ����ã�
����ã�![]() ��
��
����ͼ2����Q��P�����ʱ����![]() �ɵã�
�ɵã�![]() ����
����![]() �����
�����![]() ��
��
����������![]() ��
��![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij��һ����ÿ������������������¼�¼���±���
���� | һ | �� | �� | �� | �� | �� | �� |
������� | 10�� | 12�� | 11�� | 9�� | 7�� | 5�� | 7�� |
������� | 2�� | 1�� | 0�� | ��1�� | ��4�� | ��5�� | ��5�� |
���²�����һ��������_____����һ���²�Ϊ_____�森