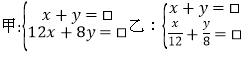题目内容
【题目】如图,点![]() 、
、![]() 、
、![]() 分别是等边
分别是等边![]() 各边上的点,且
各边上的点,且![]() ,
,![]() .
.
(![]() )求证:
)求证:![]() 是等边三角形.
是等边三角形.
(![]() )若
)若![]() ,求等边
,求等边![]() 的周长.
的周长.

【答案】(1)详见解析;(2)18
【解析】
(1)由等边三角形的性质易得AB=BC=AC,∠A=∠B=∠C=60°,由已知易得BD=CE=AF,∠DEB=∠EFC,可得△BDE≌△CEF≌△AFD,由全等三角形的性质可得DE=FD=EF,证得结论;
(2)首先由∠DEC=150°,易得∠FEC=90°,可得△ADF、△BED、△CFE均为直角三角形,可得∠CFE=∠ADF=∠BDE=30°,由直角三角形的性质可得CF=AD=BE=2BD=4,可得AB,易得结果.
(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵BD=CE,
∴BD=CE=AF,
在△BDE与△CEF中,
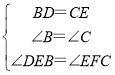 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
同理可得△BDE≌△AFD,
∴DE=FD,
∴DE=FD=EF,
∴△DEF为等边三角形;
(2)解:∵∠DEC=150°,∠DEF=60°,
∴∠FEC=90°,
∴△ADF、△BED、△CFE均为直角三角形,且∠CFE=∠ADF=∠BDE=30°,
∵BD=CE=2,
∴CF=AD=BE=2BD=4,
∴AB=BC=AC=6,
∴等边△ABC的周长为:6×3=18

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目