题目内容
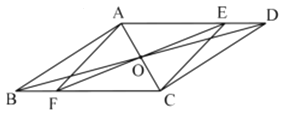
【题目】如图 ,在平行四边形 ABCD 中,对角线 AC 、 BD 交于点 O ,并且 DAC 60 ,ADB 15 ,点 E 是 AD 上一动点,延长 EO 交 BC 于点 F 。当点 E 从 D 点向 A 点移动 过程中(点 E 与点 D 、点 A 不重合),则四边形 AFCE 的变化是( )
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
【答案】C
【解析】
在整个运动过程中,始终有AO=CO,EO=FO,所以四边形AFCE恒为平行四边形,再考查四边形AFCE的对角线AC与EF,会发现随着点E的运动,它们满足AC、EF既不垂直也不相等![]() AC⊥EF
AC⊥EF![]() AC、EF既不垂直也不相等
AC、EF既不垂直也不相等![]() AC=EF
AC=EF![]() AC、EF既不垂直也不相等的过程,由此进行判断即可.
AC、EF既不垂直也不相等的过程,由此进行判断即可.
解:在整个运动过程中,始终有AO=CO,EO=FO,所以四边形AFCE恒为平行四边形.
∵DAC 60,ADB 15,∴∠AOD=180°-∠DAC-∠ADB=105°.
点E从D点向A点移动过程中,当∠EOD<15°时,AC、EF既不垂直也不相等,四边形AFCE为平行四边形,
当∠EOD=15°时,AC⊥EF,四边形AFCE为菱形,
当15°<∠EOD<45°时,AC、EF既不垂直也不相等,四边形AFCE为平行四边形,
当∠EOD=45°时,∠AEO=60°,∵DAC 60,∴∠AEO=DAC,
∴AO=EO,∴AC=EF,∴四边形AFCE为矩形,
当45°<∠EOD<105°时,AC、EF既不垂直也不相等,四边形AFCE为平行四边形,
故选B.

练习册系列答案
相关题目