Question

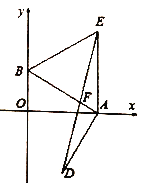
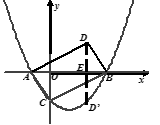
【题目】如图，抛物线y＝x2－x＋a与x轴交于点A，B，与y轴交于点C，其顶点在直线y＝－2x上．

【1】求a的值；

【2】求A，B的坐标；

【3】以AC，CB为一组邻边作□ACBD，则点D关于x轴的对称点D′ 是否在该抛物线上？请说明理由．

Answer 1

【答案】

【1】抛物线的顶点坐标为(1,a－)

∵顶点在直线y＝－2x上，∴a－＝－2．即a＝－

【2】由（1）知，抛物线表达式为y＝x2－x－ ，

令y＝0，得x2－x－ ＝0．解之得：x1＝－1，x3＝3．

∴A的坐标 (－1,0)，B的坐标 (3,0)；

【3】∵四边形ABCD是平行四边形，

∴点C，D关于对角线交点(1,0)对称又∵点D′ 是点D关于x轴的对称点，点C，D′ 关于抛物线的对称轴对称．∴D′ 在抛物线上．

【解析】（1）根据抛物线的顶点在直线y＝－2x上，运用待定系数法求得

（2）由（1）得抛物线的解析式，因为A，B的坐标在x轴上，所以纵坐标为0，代入抛物线的解析式，解一元二次方程可求得A，B的坐标

（3）由平行四边形知C，D关于对角线交点对称，通过点D′ 是点D关于x轴的对称点，可知点C，D′ 关于抛物线的对称轴对称，即可得出结论