题目内容
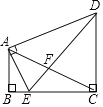
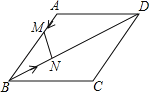
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=3![]() cm,AC=6cm,将△ABC绕点C逆时针旋转90°后得到△A1B1C,再将△A1B1C沿CB向右平移,使点B2恰好落在斜边AB上,A2B2与AC相交于点D.
cm,AC=6cm,将△ABC绕点C逆时针旋转90°后得到△A1B1C,再将△A1B1C沿CB向右平移,使点B2恰好落在斜边AB上,A2B2与AC相交于点D.
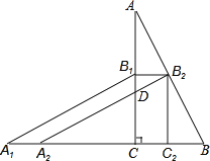
(1)判断四边形A1A2B2B1的形状,并说明理由;
(2)求△A2CD的面积.
【答案】(1)四边形A1A2B2B1是平行四边形,理由见解析;(2)![]() =
=![]() cm2.
cm2.
【解析】
(1)根据平移的性质以及平行四边形的判定定理,即可得到结论;
(2)根据勾股定理得BC=3cm,进而得CB1=3cm,AB1=3cm,B1B2 =![]() cm,A1 A2=
cm,A1 A2=![]() cm,CA2=
cm,CA2=![]() cm,由A1B1∥A2B2,得
cm,由A1B1∥A2B2,得![]() =
=![]() ,从而得CD=
,从而得CD=![]() cm,进而即可求解.
cm,进而即可求解.
(1)四边形A1A2B2B1是平行四边形,理由如下:
∵将△ABC绕点C逆时针旋转90°后得到△A1B1C,再将△A1B1C沿CB向右平移得△A2B2C2,
∴A1B1∥A2B2,A1B1=A2B2,
∴四边形A1A2B2B1是平行四边形;
(2)在Rt△ABC中,BC=![]() =
=![]() =3cm,
=3cm,
由题意:BC=CB1=3cm,A1C=AC=6cm,
∴AB1=3cm,
∵B1B2∥BC,AB1=CB1,
∴AB2=B2B,
∴B1B2=![]() BC=
BC=![]() cm,
cm,
∴A1 A2= B1B2 =![]() cm,
cm,
∴CA2=6-![]() =
=![]() cm,
cm,
∵A1B1∥A2B2,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴CD=![]() cm,
cm,
∴![]() =
=![]() CA2CD=
CA2CD=![]() ×
×![]() ×
×![]() =
=![]() cm2.
cm2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目