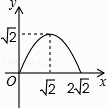题目内容
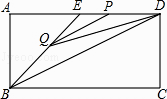
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 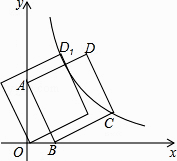
【答案】2
【解析】解:对于直线y=﹣3x+3,
令x=0,得到y=3;令y=0,得到x=1,即A(0,3),B(1,0),
过C作CE⊥x轴,交x轴于点E,过A作AF//x轴,过D作DF垂直于AF于F,如图所示,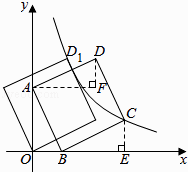
∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∴∠OAB+∠ABO=90°,∠ABO+∠EBC=90°,
∴∠OAB=∠EBC,
在△AOB和△BEC中,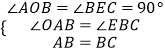 ,
,
∴△AOB≌△BEC(AAS),
∴BE=AO=3,CE=OB=1,
∴C(4,1),
把C坐标代入反比例解析式得:k=4,即y= ![]() ,
,
同理得到△DFA≌△BOA,
∴DF=BO=1,AF=AO=3,
∴D(3,4),
把y=4代入反比例解析式得:x=1,即D1(1,4),
则将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,即a=2,
(k≠0)上的点D1处,即a=2,
故答案为:2.
对于直线解析式,分别令x与y为0求出y与x的值,确定出A与B坐标,后根据三角形全等得出C点坐标,进而求出反比例函数的解析式,进而确定D点的坐标和D1点的坐标,即可确定出a的值.

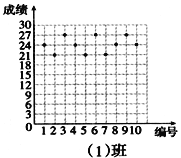
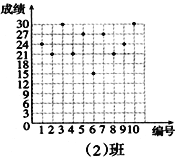
【题目】王老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年(1)班和八年(2)班进行了检测。如图所示表示从两班随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
班级 | 平均分(分) | 中位数(分) | 众数(分) |
八年(1)班 | 24 | 24 | |
八年(2)班 | 24 |
(2)你认为那个班的学生纠错的得分情况比较整齐一些,通过计算说明理由.
【题目】阅读下面材料:
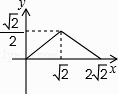
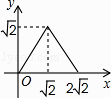
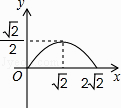
小明想探究函数![]() 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |

小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数![]() 的一条性质:_____________.
的一条性质:_____________.