题目内容
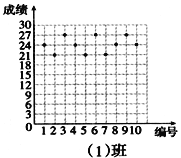
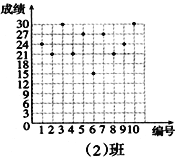
【题目】王老师为了了解学生在数学学习中常见错误的纠正情况，收集整理了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对他所教的八年（1）班和八年（2）班进行了检测。如图所示表示从两班随机抽取的10名学生的得分情况：
（1）利用图中提供的信息，补全下表：
班级 | 平均分（分） | 中位数（分） | 众数（分） |
八年（1）班 | 24 | 24 | |
八年（2）班 | 24 |
（2）你认为那个班的学生纠错的得分情况比较整齐一些，通过计算说明理由.
【答案】（1）八年（1）班的平均数为24，八年（2）班的中位数为24，众数为21;（2）八年（1）成绩比较整齐.
【解析】（1）分别根据平均数、中位数、众数的定义逐一进行求解即可得；
（2）根据方差的公式分别计算两个班的方差进行比较即可得.
（1）由图可知八年（1）班的成绩分别为24、21、27、24、21、27、21、24、27、24，
所以八年（1）班的平均数分为（24+21+27+24+21+27+21+24+27+24）÷10=24分，
八年（2）班的成绩从小到大排列为：15、21、21、21、24、24、27、27、30、30，
八年（2）班的中位数为24，众数为21；
（2）
，
，
∵
<
，
∴ 八年（1）成绩比较整齐.
【题目】甲、乙两校的学生人数基本相同，为了解这两所学校学生的数学学业水平，在同一次测试中，从两校各随机抽取了30名学生的测试成绩进行调查分析，其中甲校已经绘制好了条形统计图，乙校只完成了一部分．
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
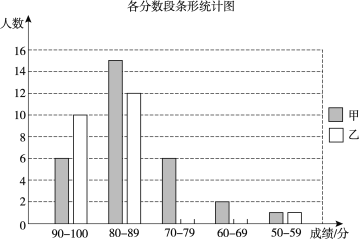
（1）请根据乙校的数据补全条形统计图；
（2）两组样本数据的平均数、中位数、众数如下表所示，请补全表格；
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
（3）两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些，
请为他们各写出一条可以使用的理由；
甲校： ．乙校： ．
（4）综合来看，可以推断出 校学生的数学学业水平更好一些，理由为 ．
